Tension Force
Tension or tensile force in a rope or stand that results from that object being stretched. See how to approach a variety of tension problems here.
Tension (FT) is the pulling force exerted by a strand (ie. string) in the opposite direction of a force applied. (Unit: N)
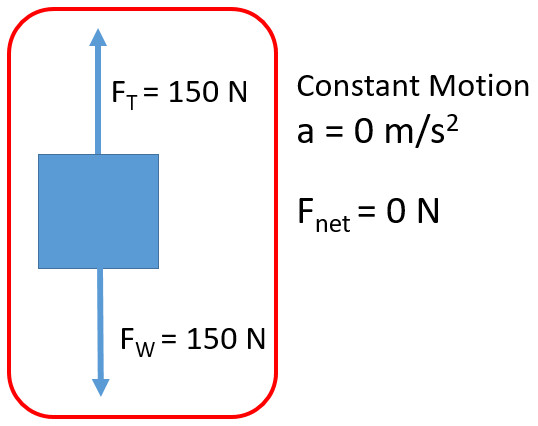
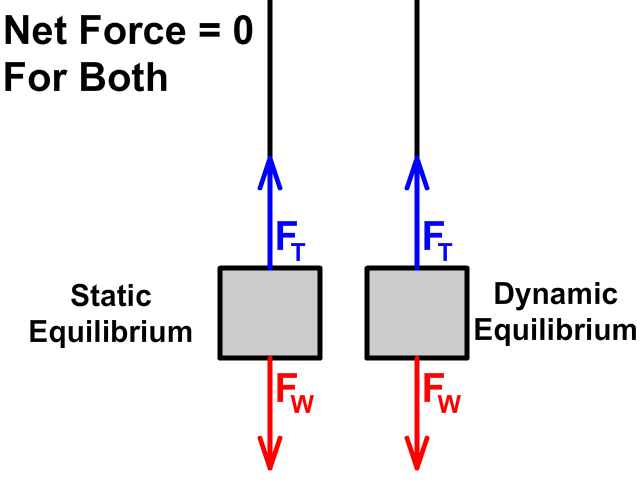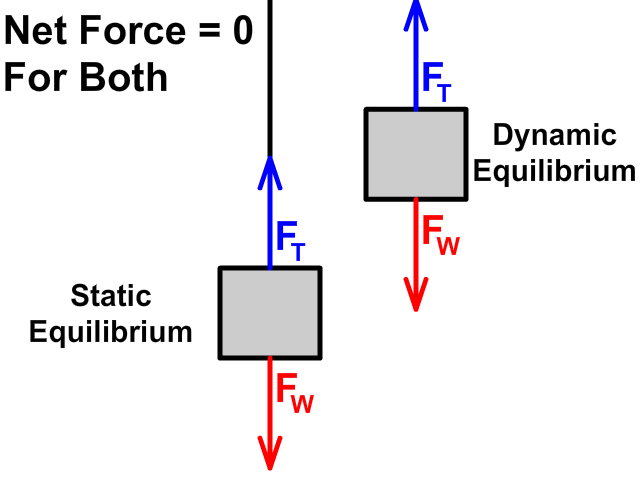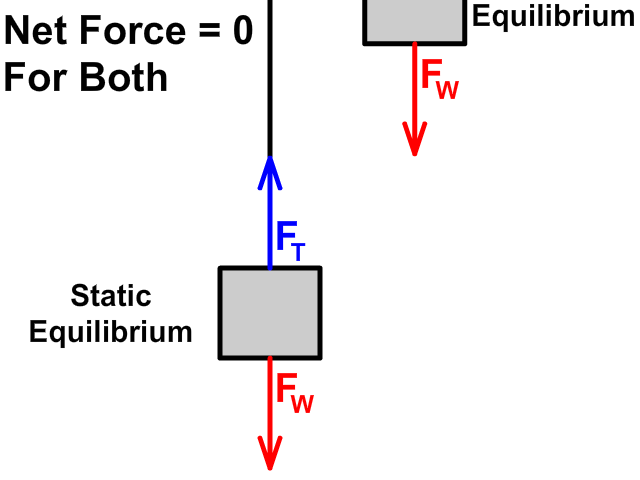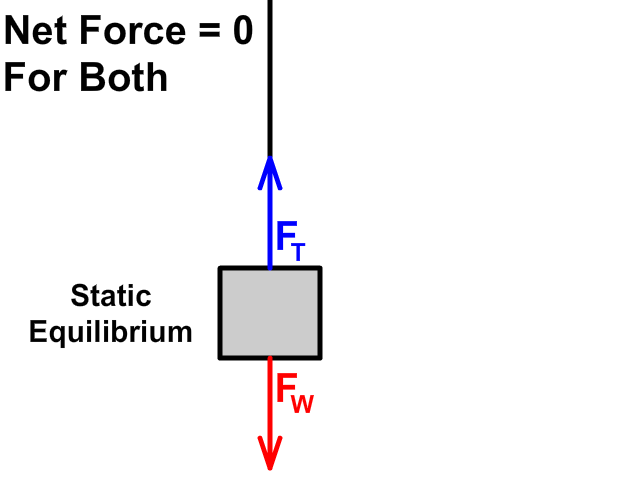
When tension up is equal to weight down
There is no net force and therefore no acceleration. The state of motion remains. Inertia would keep a moving object moving and an object at rest would remain at rest.
- Static Equilibrium: When tension up is equal to weight down but the object is at rest (no motion)
- Dynamic Equilibrium: When tension up is equal to weight down an object moves with constant velocity
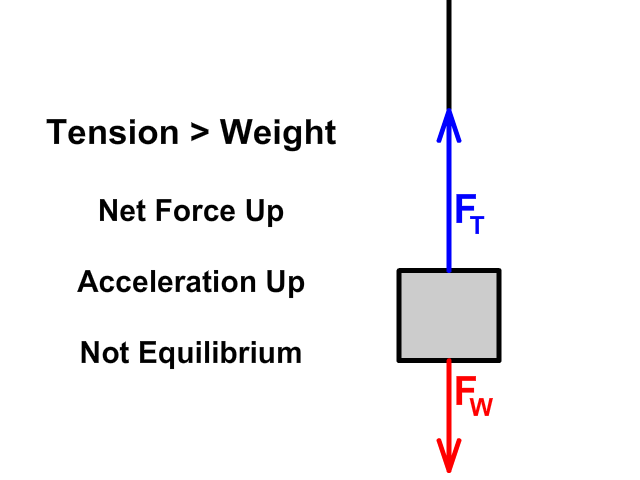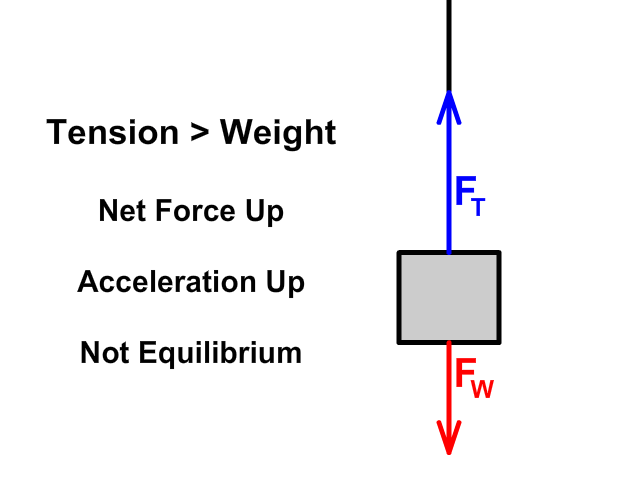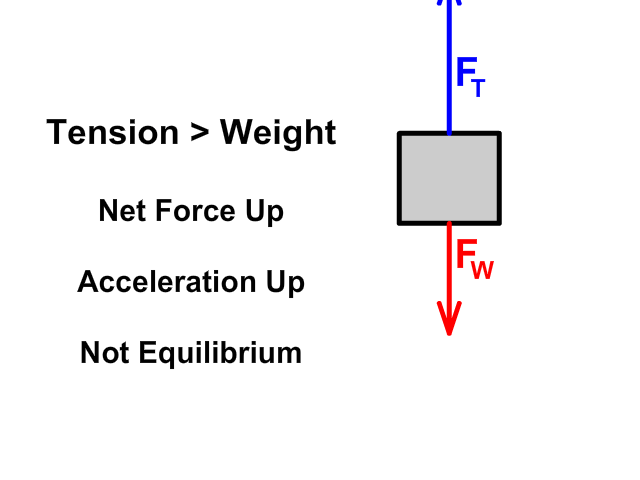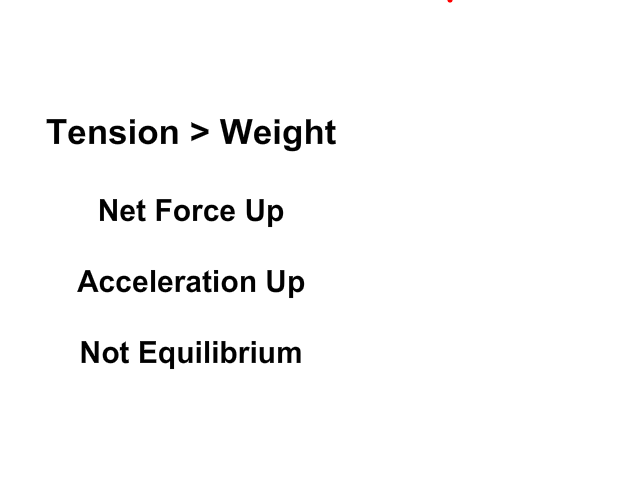
When tension up is greater than weight down
- Net force (Fnet) would be up
- An object would accelerate up
- The amount of acceleration would depend on mass (m) following Newton's Second Law (Fnet = ma)
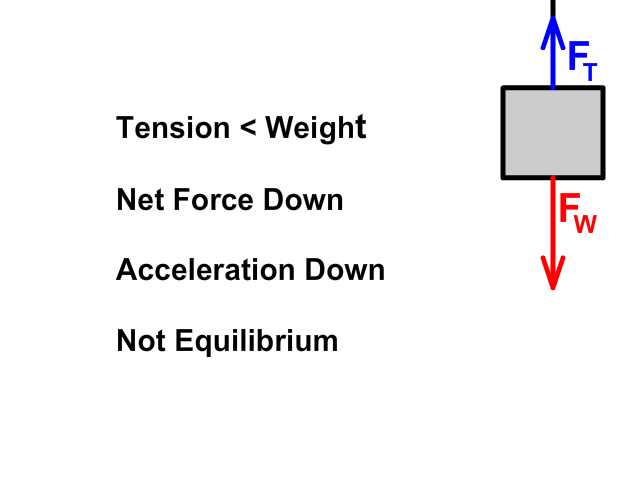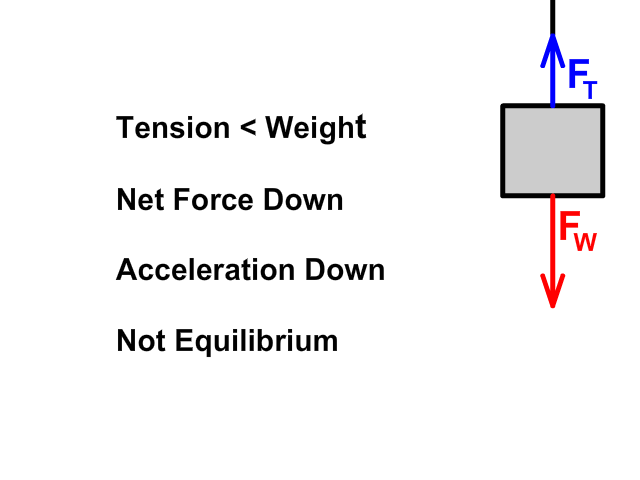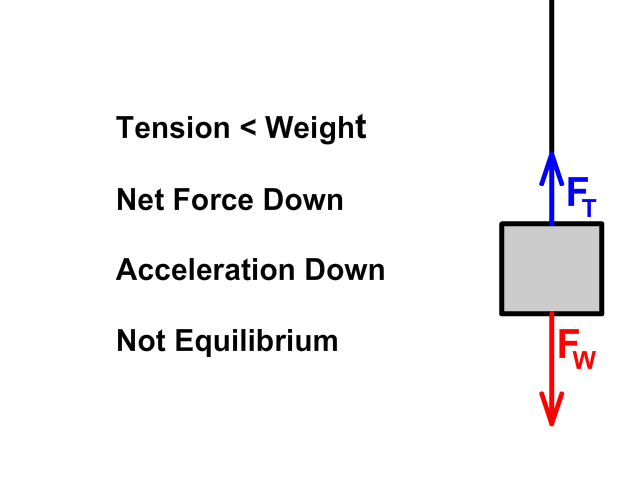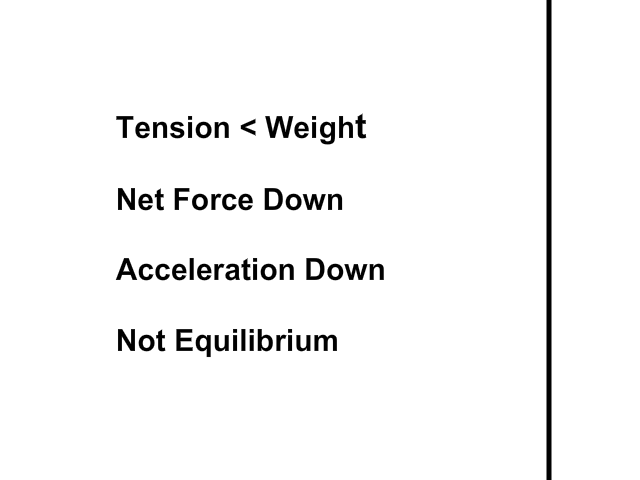
When tension up is less than weight down
- Net force (Fnet) would be down
- An object would accelerate down
- The amount of acceleration would depend on mass (m) following Newton's Second Law (Fnet = ma)
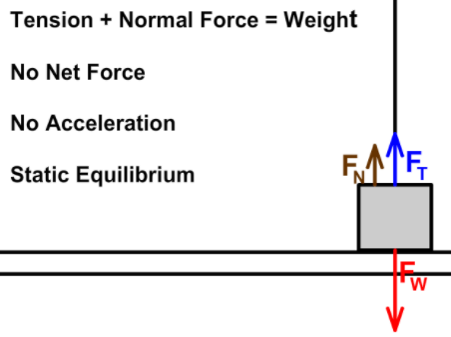
When tension up is less than weight down but on a horizontal surface
- If the object comes to rest on a horizontal surface, normal force would make up the difference putting the system in equilibrium
- FT + FN = -FW
- Tension and normal force up would equal the magnitude of weight down. The negative in the equation representing the opposite direction
Example Problems
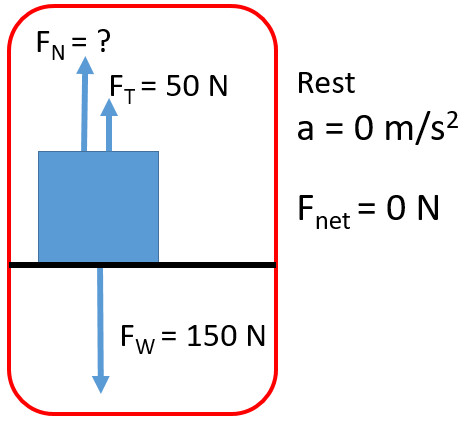
Q1: What is the tension in the rope necessary to lift a 150 N object at a constant velocity up?
Q2: What is the normal force of a 15 kg object when on the ground and a rope with 50N of tension is pulling up?
Tension with Multiple Vertical Ropes
When there is one rope up all of the weight is supported by that one rope and the tension is equal to weight.
When there are multiple ropes all directed straight up each will support an equal amount of weight. To find this you would divide the weight by number of strands.
Q3: Susie, who weighs 650 N, suspends herself from the monkey bars holding herself up with both hands horizontal. What is the tension in each arm?
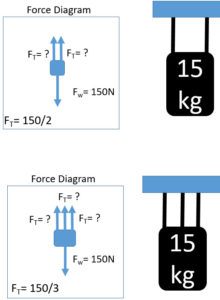
Divide by the number of ropes for tension in each when you have multiple ropes suspending an object vertically.
Tension at Equal Angles From the Vertical
As the angle from the vertical increases tension increases. Tension is the most when the painting is at the highest point in the animation and the angle (Ө) is the most.
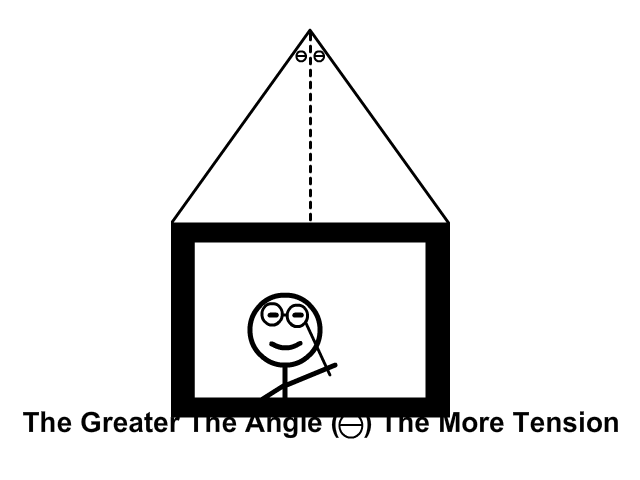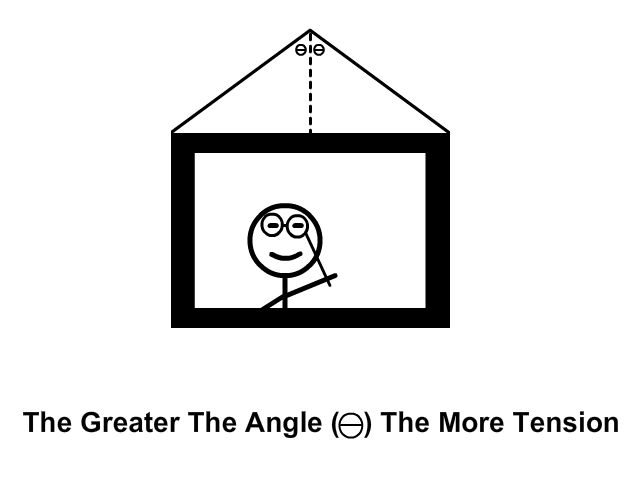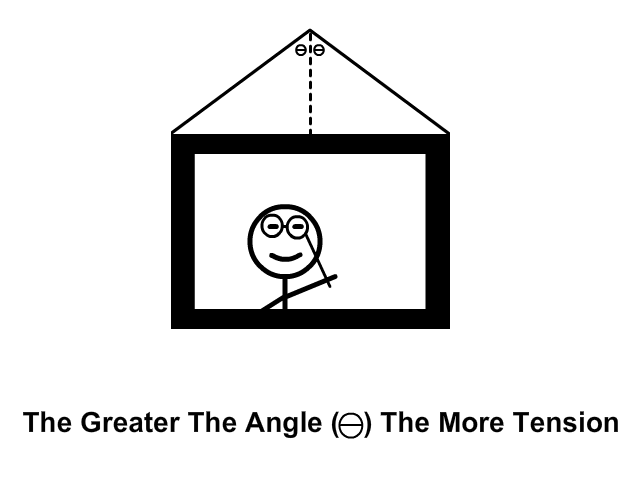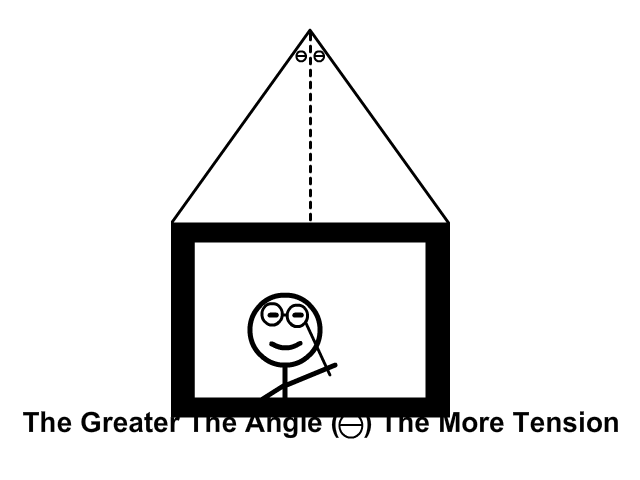
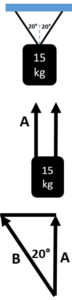
Calculating Tension When at Equal Angles From the Vertical
How to solve tension at an angle when at equal angles.
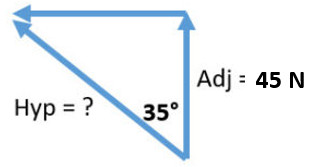
A. Figure what each rope has to lift vertically
B. Solve for the hypotenuse for the tension this individual rope
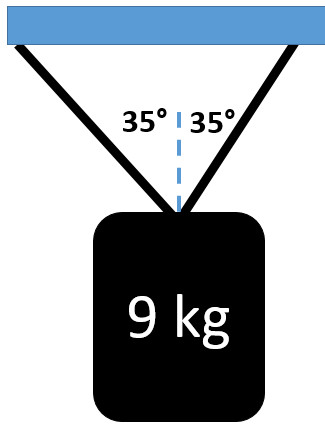
Q4: What is the tension in each of two ropes holding up a 9 kg mass at 35° from the vertical as seen to the right
- Continue to Forces on an Incline Plane
- Back to the Main Forces Page
- Back to the Stickman Physics Home Page
- Equation Sheet