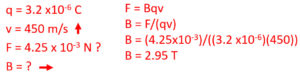Force on a Moving Charge

A force on a moving charge is maximum when created by a magnetic field perpendicular to the moving charge. Learn to calculate force and determine direction.

Variables Used in this Force on a Moving Charge Page

	Variable	MKS Unit	Unit Abbreviation
Charge	q	Coulomb	C
Current	I	Ampere	A
Force	F	Newton	N
Length	L	Meter	m
Magnetic Field	B	Tesla	T
Velocity	v	Meters per second	m/s

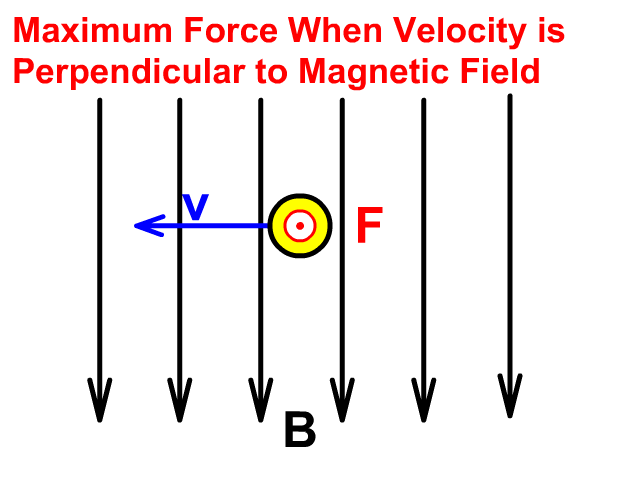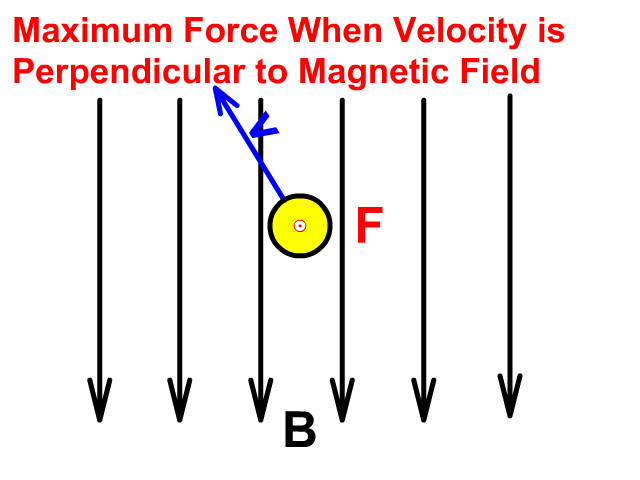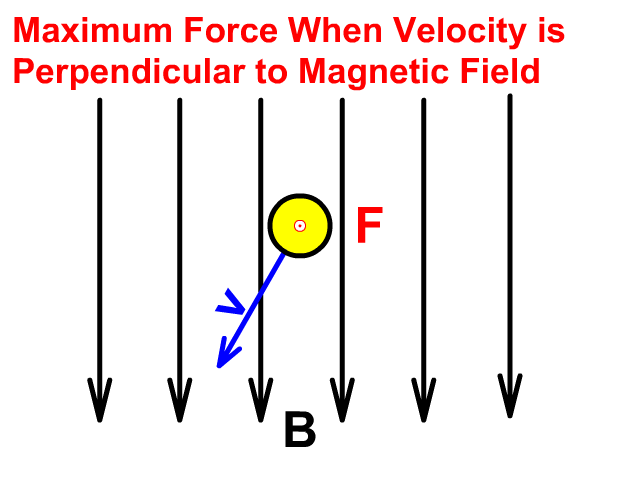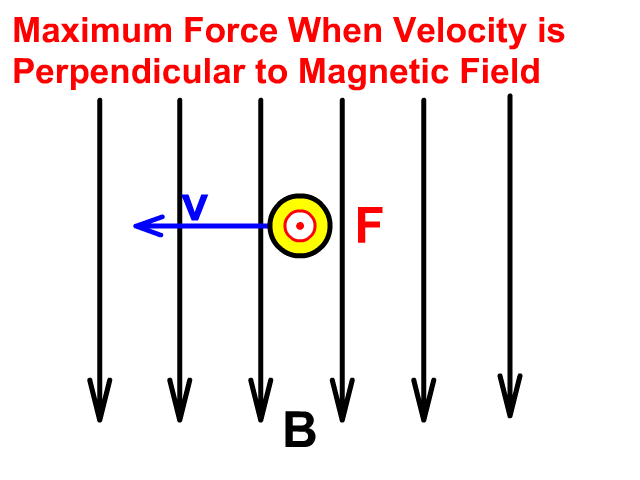
Force on Charge Moving in a Magnetic Field

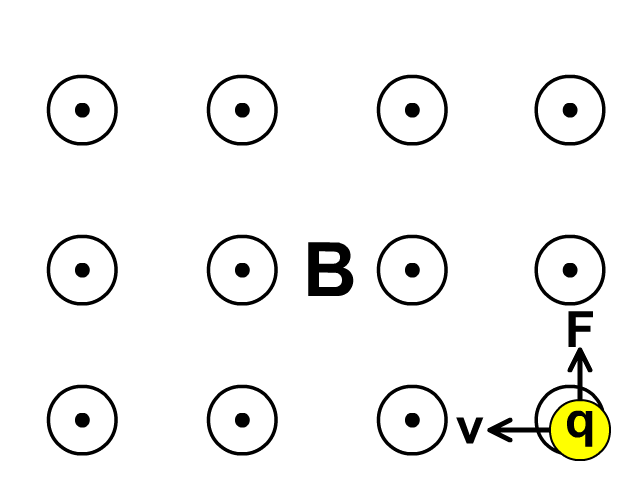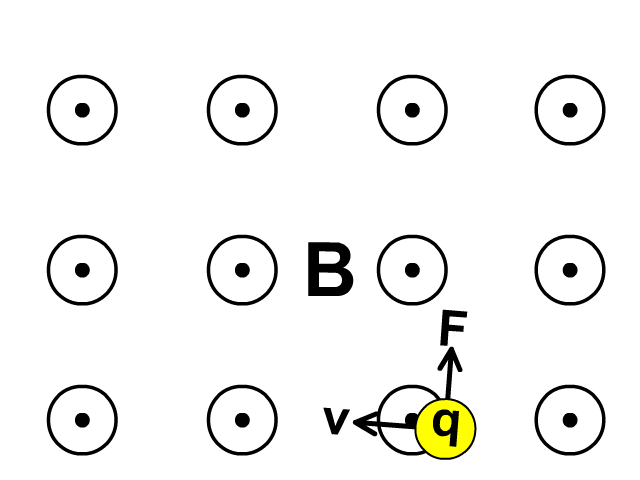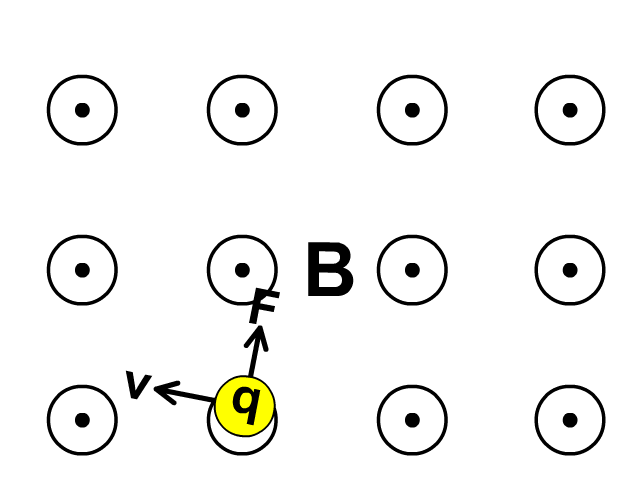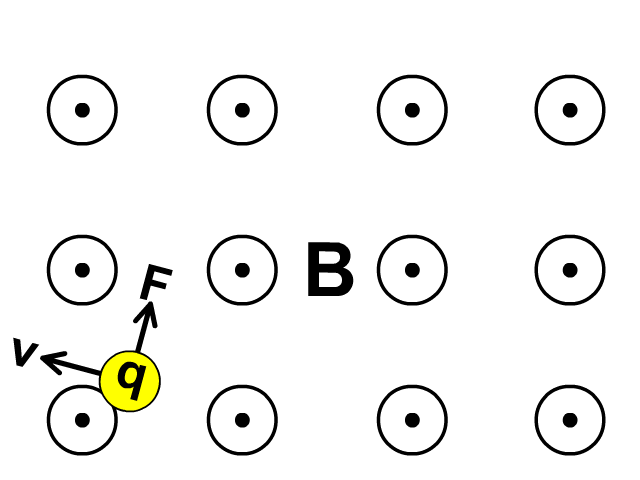
A force (F) on a moving charge (q) will be maximum at a velocity (v), perpendicular to Magnetic Field (B).

Force will be less with velocity at any angle less than perpendicular to the magnetic field and no force is present when velocity is parallel.

The amount of the force relates to the size of magnetic field, the magnitude of charge, and the velocity it is moving.

This equation represents the relationship:

F = Bqv

force = (magnetic field)(charge)(velocity)

Observe in the animation that the screen has a magnetic field towards you (circle with a dot represents towards you). The particle moving left creates a force up. The direction of force causing acceleration changes as velocity changes curving upward in this field.

Maximum Force When Velocity or Current is Perpendicular

On this page, we will stick to simple mathematical problems with charge traveling perpendicular to a magnetic field.

A charge or current moving parallel to the magnetic field would have no force. Any velocity between perpendicular and parallel would only have the perpendicular component used in the solution for force.

maximum force with velocity perpendicular to the magnetic field

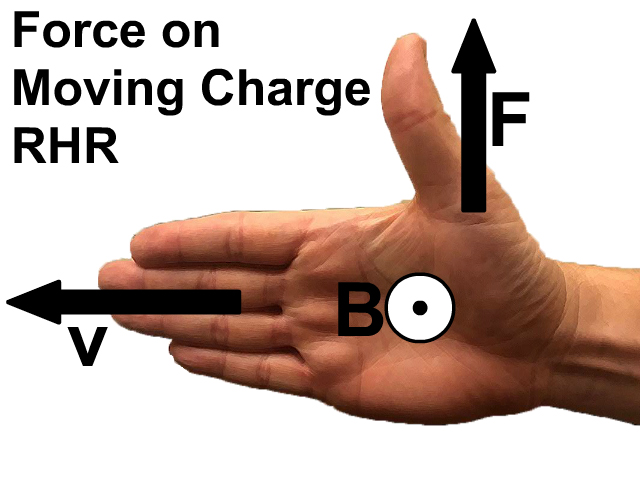
Moving Positive Charge in a Magnetic Field Right Hand Rule (RHR)

When determining the direction of force, velocity, or magnetic field for a positive charge you can use a right hand rule mnemonic. This may be used in conjunction with F=Bqv equation to determine direction of a variable.

(Version 1)

When holding your hand open with your thumb up at a right angle to your fingers:

Force: the direction of your thumb
Magnetic Field: the direction your palm is facing
Velocity: the direction of your fingers for the positive charge

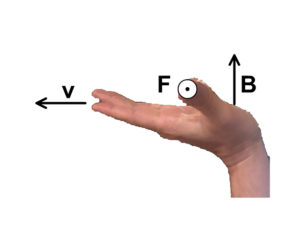
(Version 2) of the Same Positive Moving Charge in a Magnetic Field RHR

Depending on your teacher they may have taught you an alternate version of the previous right hand rule. Both show the exact same relationship between magnetic field, force, and velocity.

Force: the direction of your thumb
Velocity: the direction of your pointer finger
Magnetic Field: the direction of your middle finger

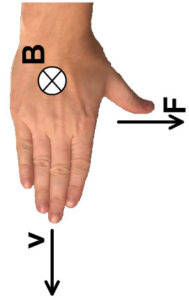
Exception to the RHR for a Negative Charge

Some questions will have an electron or negative charge moving in a magnetic field. If you see this in a problem, use your left hand instead of your right. So when using the left hand of version 1 of the right hand rule for charge moving in a magnetic field:

Force: the "left hand" thumb
Magnetic Field: "left hand" palm
Velocity: "left hand" fingers will represent the velocity of the negative charge.

Example Problems

1. What direction is a positive charge moving if force is going to the right and the magnetic field is directed away from you into the page?

Down the screen

You have a positive charge so use your right hand

2. What direction is force, if a negative charge is moving in a magnetic field directed upwards to the top of the page and the velocity is left?

Out of the screen towards you

Here you have a negative charge so use your left hand.

3. What direction is the magnetic field if a proton has a velocity is into the page away from you and force is directed down the page?

Right

A proton is a positive charge so use your right hand

4. Would a particle have a positive or negative charge if force is directed down the page when the particle was moving out of the page towards you in a magnetic field to the right?

negative

Test this out with your right hand. When your right hand fingers (velocity) are pointed towards you and your thumb is down, your palm is to the left, not right. You know its a negative charge since this contradicts what a positive charge would do.

5. What is the magnitude of force when a 2.51 C charge is traveling 422 m/s perpendicular to a magnetic field of 2.20 T?

F = ?

q = 2.51 C

v = 422 m/s

B = 2.20 T

F = Bqv

F = (2.20)(2.51)(422) = 2330 N

6. A charge of +3.2 x10^-6 C is traveling at north at 450 m/s in a magnetic field to the east. The magnetic force it experiences is 4.25 x 10^-3 N. What is the strength of the magnetic field and direction of the force?

The magnetic field is 2.95 T

The force is directed down into the ground.

It's a positive charge so use your right hand. When your fingers (velocity) are facing north and your palm is facing east, your thumb is pointed down into the ground.

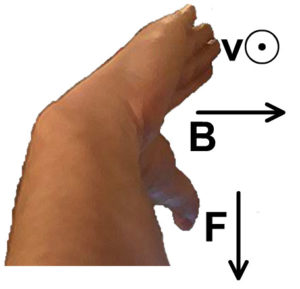
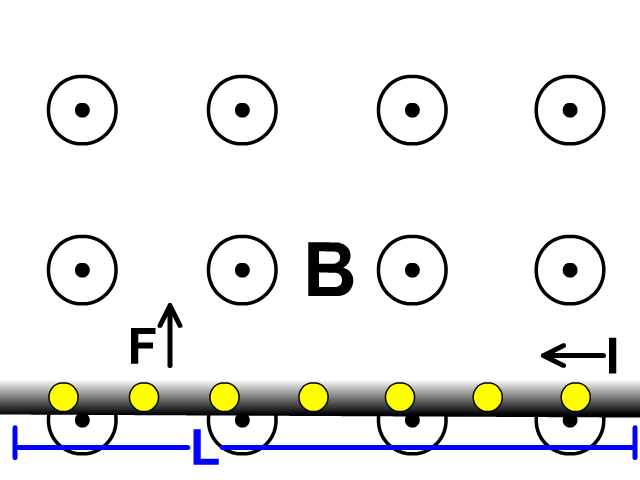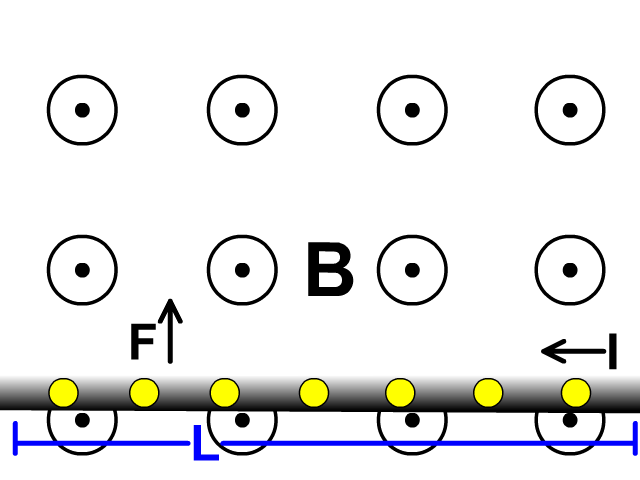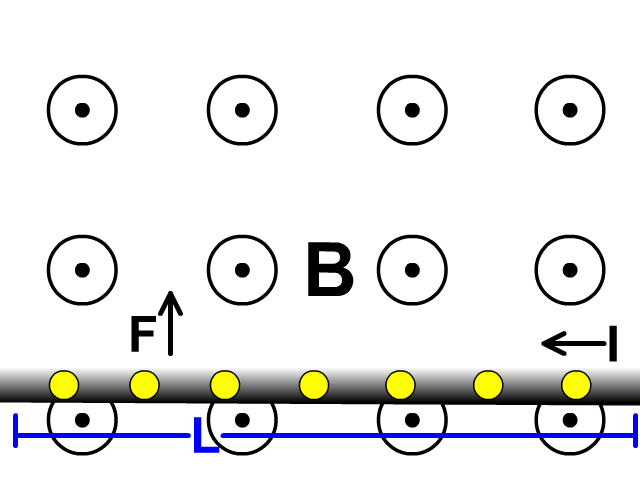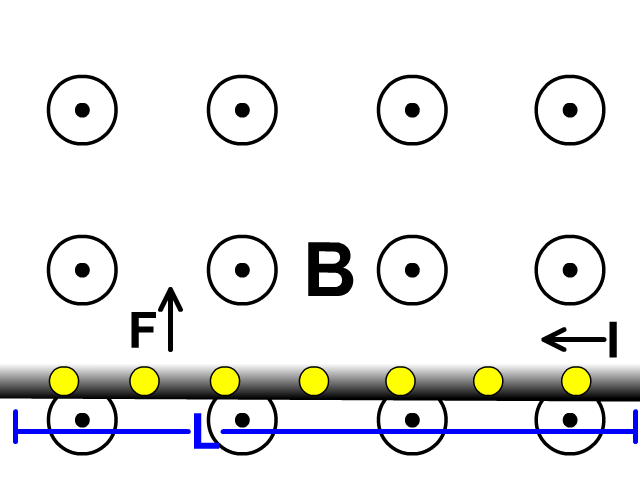
Force on Wire Carrying Current in a Magnetic Field

A moving charge can be represented by a current (I) in a length of wire (L) perpendicular to a magnetic field. This would also have a maximum force (F) when perpendicular to a magnetic field magnetic field (B).

This equation represents the relationship:

F = BIL

force = (magnetic field)(current)(length of wire)

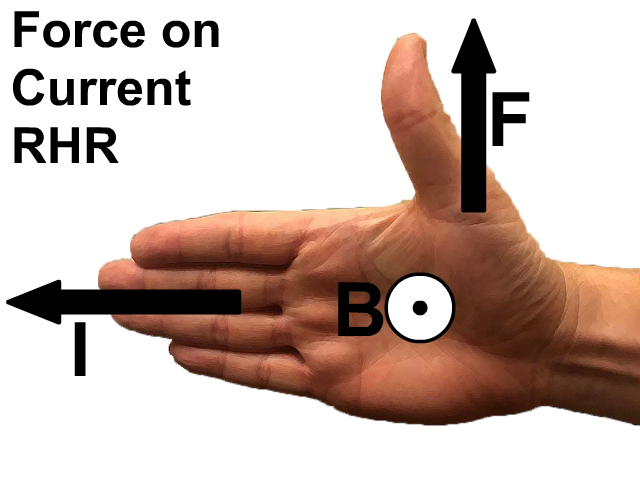
Force on a Wire Carrying Current in a Magnetic Field RHR

Conventional current involves a positive flow of charge so this right hand rule is very similar to the right hand rule for a moving positive charge.

Here you replace the fingers representing which was velocity before for current. This right hand rule would be used in conjunction with F = BIL to determine the direction of one of the variables.

When holding your hand open with your thumb up at a right angle to your fingers:

Force: the direction of your thumb
Magnetic Field: the direction your palm is facing
Current: the direction of your fingers

Current in a Magnetic Field Right Hand Rule

Example Problems

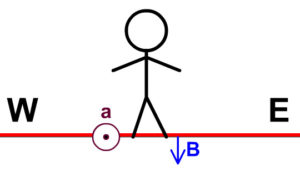
7. A current carrying wire lies horizontally in front of you west to east on the ground. If the magnetic field is directed into the ground and the wire accelerates toward you, in which direction is the current flowing? (Note: Force causes acceleration so the force in the wire is towards you)

Left

Force causes acceleration so saying the acceleration down into the ground is the same as saying force is into the ground.

Use your right hand and have your thumb facing towards you and make your palm face the ground. Your fingers should now be facing left.

8. An engineer want to place a wire in a magnetic field facing north so that it helps support itself in the air when current is flowing. What direction should current run in this wire? (east to west, west to east, north to south, or south to north?

The direction of force must be up into the air if it is supporting itself. Use your right hand and have your palm facing north and your thumb up. Your fingers are now facing east. So the answer is west to east.

9. What is the magnitude of force in 10.0 meter wire with 5.00 amps of current traveling perpendicular to a 2.10 T magnetic field?

F = ?

L = 10.0 m

I = 5.00 A

B = 2.10 T

F = BIL

F = (2.1)(5.0)(10.0) = 105 N

10. How much current would be traveling perpendicular to a 1.70 T magnetic field when a force of 50.0 N is present in an 80.0 meter wire?

I = ?

B = 1.70 T

F = 50.0 N

L = 80.0 m

F = BIL

I = (F)/((B)(L))

I = (50.0)/((1.70)(80.0)) = 0.368 A