Collisions and Conservation of Momentum
Momentum is conserved in a system. See how the conservation of momentum equation is applied to elastic and inelastic collisions.
Learning Targets
- I understand that momentum is conserved
- I can use the conservation of momentum equation in various situations
- I know the difference between elastic and inelastic collisions
- I can solve for variables in elastic and inelastic collisions
| Name | Variable | MKS Unit | Unit Abbreviation |
| Momentum | p | kilograms times meters per second | kg∙m/s |
| Mass | m | kilogram | kg |
| Velocity | v | meters per second | m/s |
Conservation of Momentum
Conservation of Momentum: within a system momentum is conserved
-
- Reminder: momentum is the product of mass and velocity (p=mv)
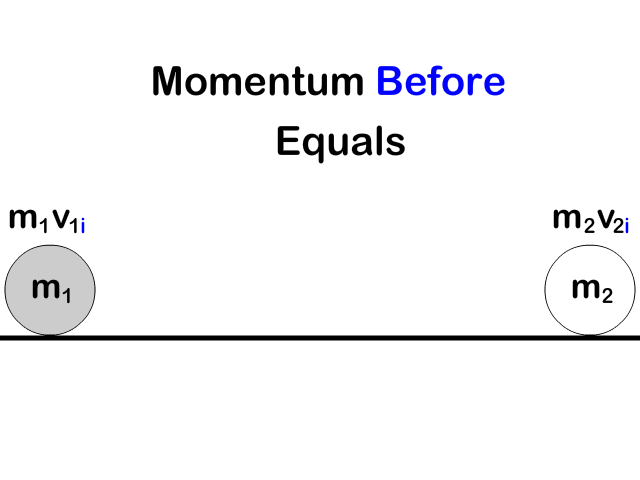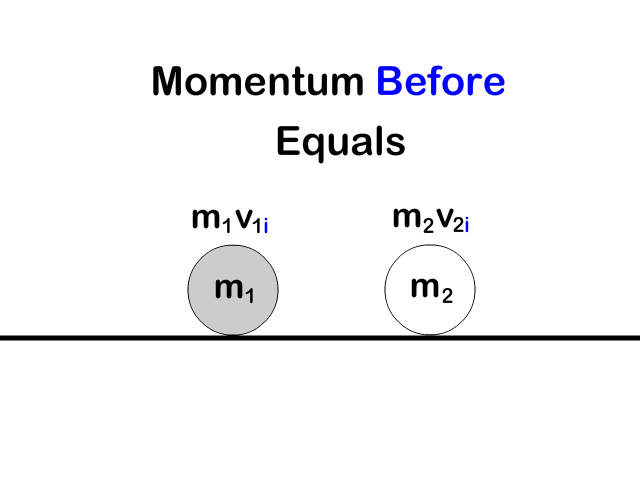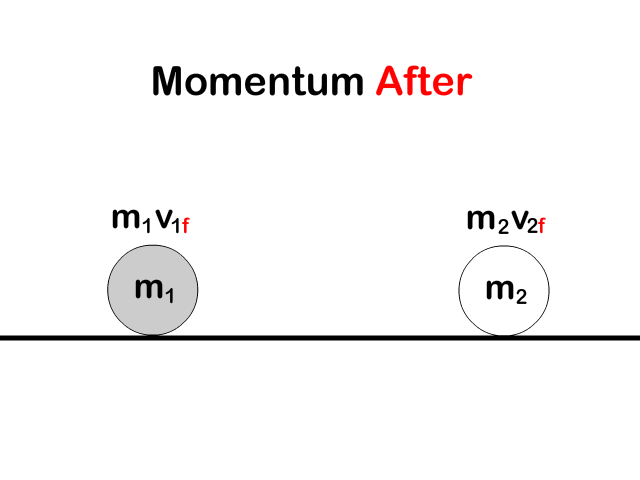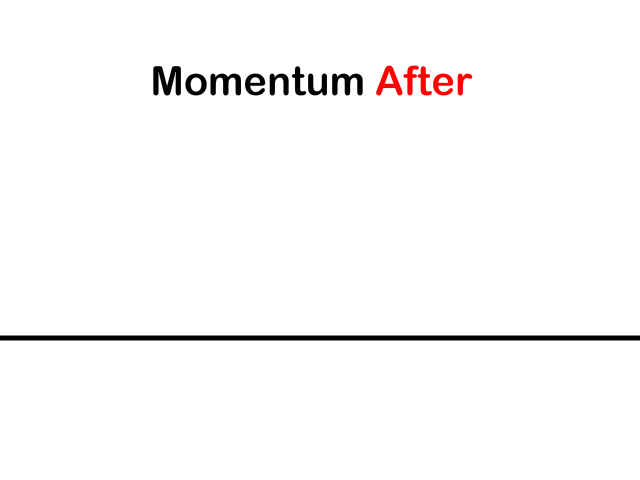
Conservation of Momentum Equation
All the momentum in the objects before equals all the momentum in the objects after an interaction
p1i + p2i = p1f + p2f
m1v1i + m2v2i = m1v1f + m2v2f
What each variable stands for
m1 : first object mass
v1i : first object initial velocity
v1f : first object final velocity
m2 : second object mass
v2i : second object initial velocity
v2f : second object final velocity
Conserved Momentum Interactions
Conserved Momentum Interactions Include:
Objects Separating
-
- Exploding
- Throwing
Starting together with a single velocity:
vi(m1 + m2) = m1v1f + m2v2f
Here you see a firecracker in one piece moving with a single velocity explode into two pieces each with its own velocity. A pitcher would begin at rest together with a baseball and after both the pitcher and baseball would have a separate velocity. We will pretend that the problems in this section occur on a frictionless surface.
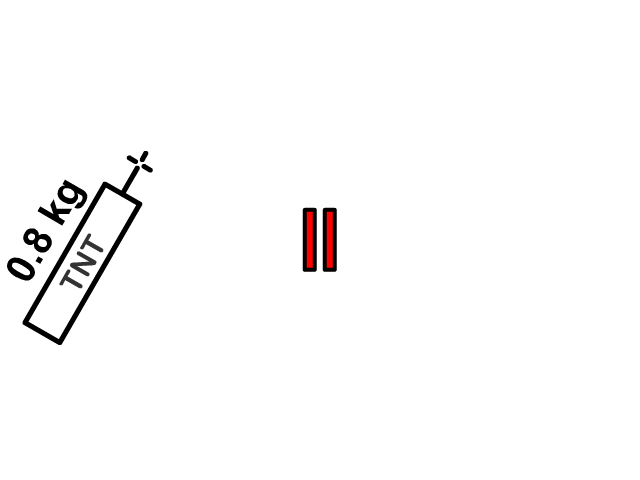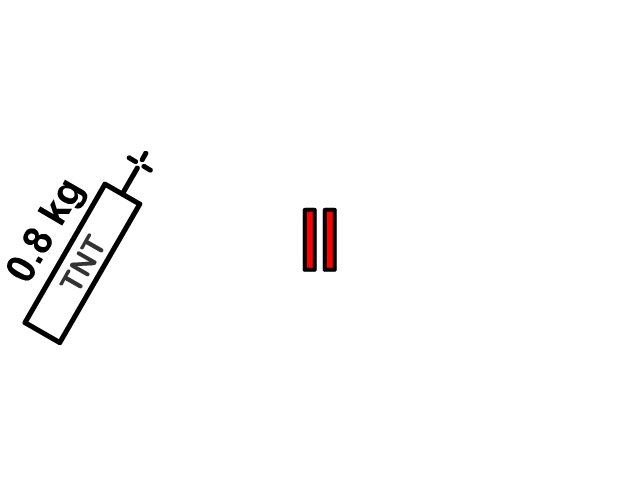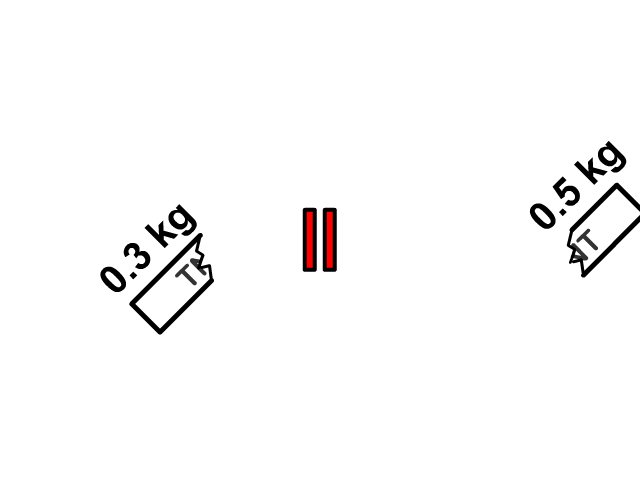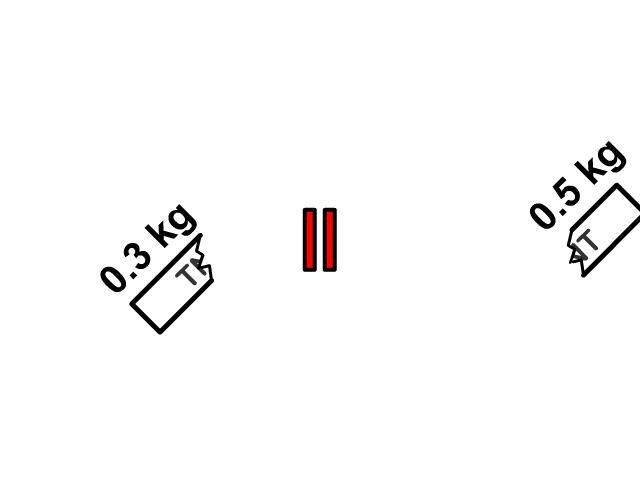
Objects Joining
-
- Catching
- Some collisions
-
- Ending together with a single velocity:
m1v1i + m2v2i = vf(m1+ m2)
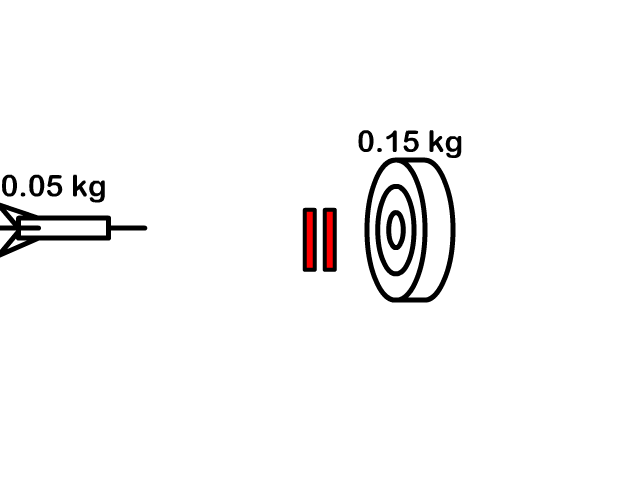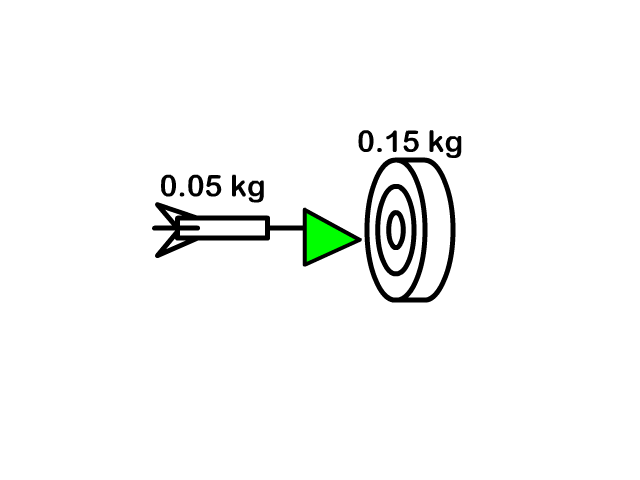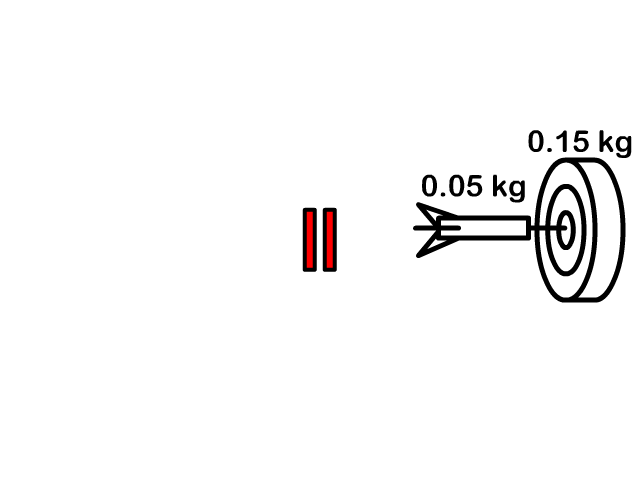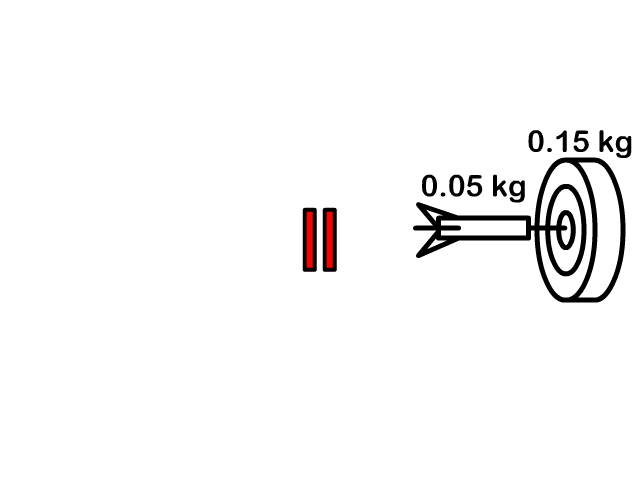
Here you see a player catch a ball each with its own velocity and together after the catch with one velocity. In another example you see a dart hit and stick into a dartboard traveling as one after the collision.

Types of Collisions
- Elastic Collision
- Momentum and kinetic energy are conserved within the system
- The original objects that collide maintain their form and do not release heat in a perfect elastic collision
Billiard balls colliding is an example of an elastic collision
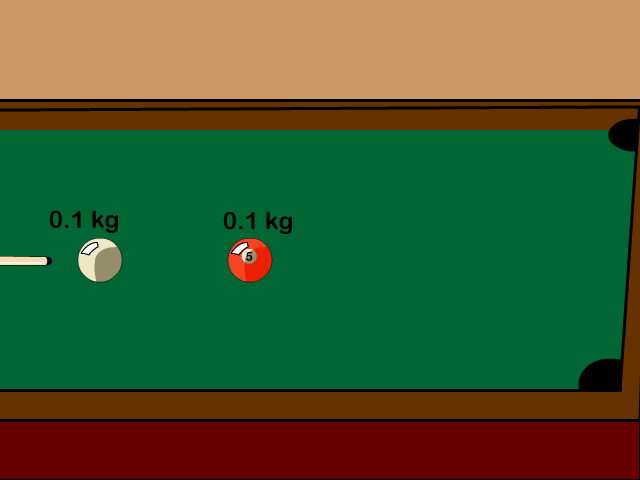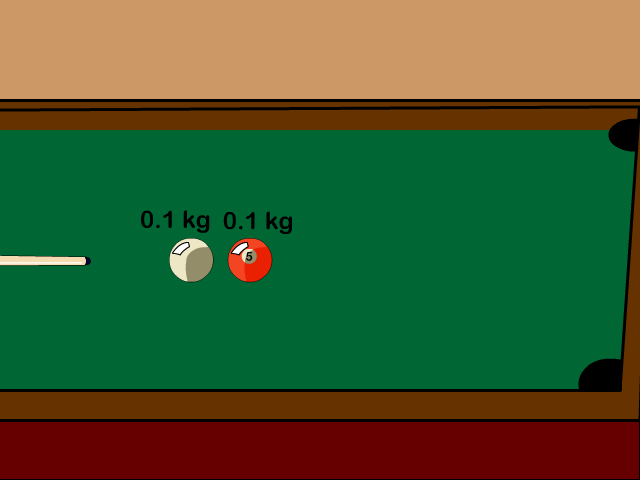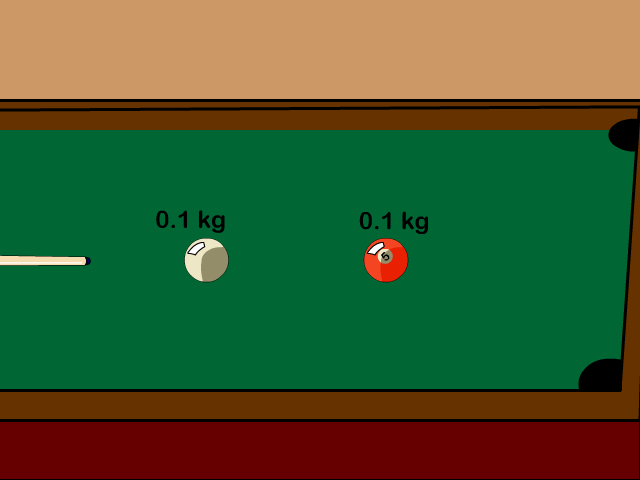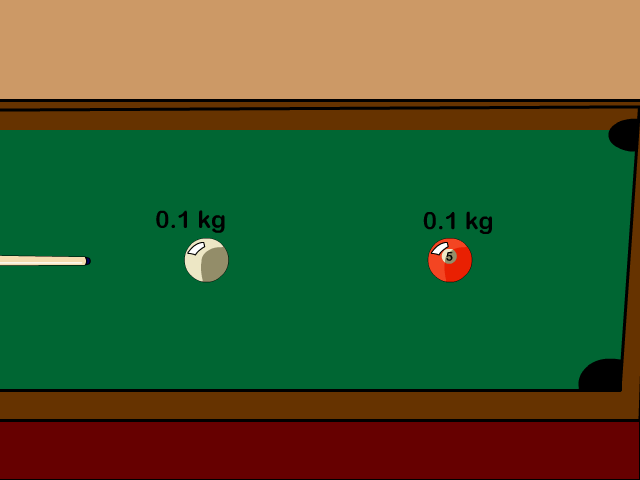
- Elastic Collision Equation
- (objects maintain form and keep separate)
m1v1i + m2v2i = m1v1f + m2v2f
- Inelastic Collision
- Momentum but not kinetic energy is conserved within the system
- Inelastic Collision Equation
- (objects combine and stick together)
m1v1i + m2v2i = vf(m1+ m2)
Q1: In which of these collisions is kinetic energy conserved? (inelastic collision, elastic collision, both)
Q2: In which of these collisions is momentum conserved? (inelastic collision, elastic collision, both)
Example Problems
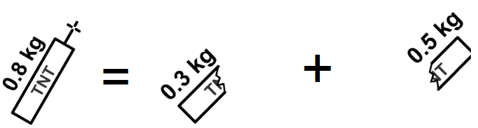
Q3: A 0.80 kg firecracker is traveling through the air at 12 m/s to the right when it explodes. After the explosion, a 0.30 kg piece of it is flying to the left at 6.0 m/s. What is the mass of the other piece and how fast is it flying?
Q4: A 95 kg pitcher at rest throws a 0.15 kg baseball 40 m/s to the right. How fast would the pitcher be going after the throw on a frictionless surface?
Q5: How fast is an 85 kg receiver traveling 6 m/s to the right going after catching a 0.43 kg football traveling at 30 m/s right?
Q6: A 0.1 kg pool ball traveling 2.5 m/s hits another 0.1 kg at rest. If the first ball stops after the elastic collision, how fast is the second now moving?
Q7: A 0.05 kg dart traveling 16 m/s hits a 0.15 kg movable target and sticks to it. How fast is the dart in the target moving together after the collision?
Conservation of Momentum Problem Set
Check out the quick check answers to see if you are correct. Watch the end of the video lesson at the top of the page to see more about the solution.
1. A 2800 kg truck moving at 12 m/s to the right hits a stopped 1100 kg car. What is the combined velocity the moment they stick together?
2. Joe has a mass of 85 kg and is at rest holding a 0.9 kg snowball. What is Joe’s velocity if he throws the snowball at 13 m/s to the right on a frictionless surface?
3. A 0.45 kg ball moving at 5.1 m/s to the right hits a 0.50 kg ball at rest. If the 0.45 kg ball is moving at 2.0 m/s right after the elastic collision, what velocity is the 0.50 kg balls velocity?
4. A 7.5 kg shopping cart is rolling at 1.0 m/s to the left at the moment you throw a 3 kg bag of flour in it at 5 m/s to the right. What is the combined velocity of the cart with a bag of flour in it?
5. A 50 kg boy is skating down the street on his 1.2 kg skateboard at 6.1 m/s to the right when he jumps off and is then going 4.0 m/s to the right. What is the velocity of the skateboard at this moment?
Links
- Back to the Main Impulse and Momentum and Conservation of Momentum Page
- Back to the Stickman Physics Home Page
- For video tutorials and other physics resources check out HoldensClass.com
- Find many of your animation resources in one place at the StickMan Physics Gallery
- Equation Sheet





