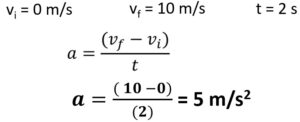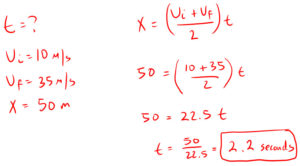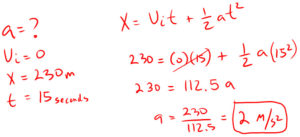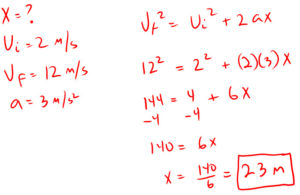Acceleration: Change in Velocity Over Time
Acceleration describes how velocity changes. This is a speeding up or slowing down which is a negative acceleration, better known as deceleration.
Learn more about acceleration and picking the right equation used in physics problems. In the next lesson we will cover the acceleration due to gravity.
Optional: Buy a guided set of notes for this page at Teachers Pay Teachers if your teacher has not provided one.
With acceleration velocity changes so never use variable v since it means constant velocity. Therefore, vi represents initial velocity and vf represents the final velocity.
Look at the animation of constant velocity compared to acceleration
Q1: Does acceleration mean you are faster?
Q2: What does acceleration mean?
Acceleration does not influence or describe instantaneous velocity
- Acceleration influences future velocity

Constant vs. Accelerated Motion
Constant Velocity Stickman
- In this animation, the stickman starts with medium velocity and ends with the exact same medium velocity since there was no acceleration
Accelerated Stickman
- In this animation, the stickman starts with low velocity and ends with the high velocity since there was acceleration
Analyzing Motion and the Direction Signs of Velocity and Acceleration
Just a reminder on directions signs from the explanations below. We will be calling right the positive direction and left the negative direction.
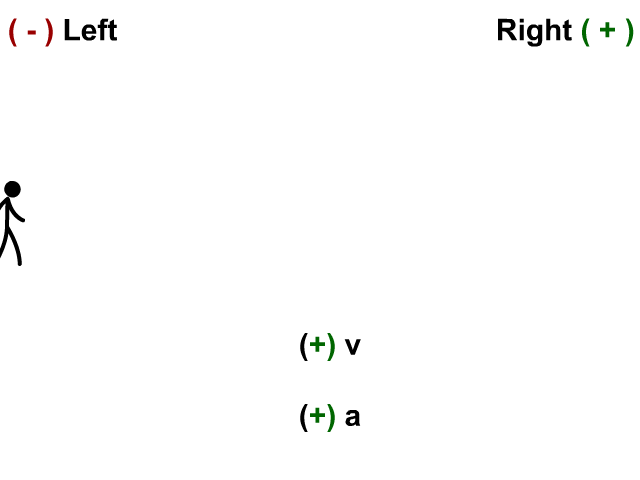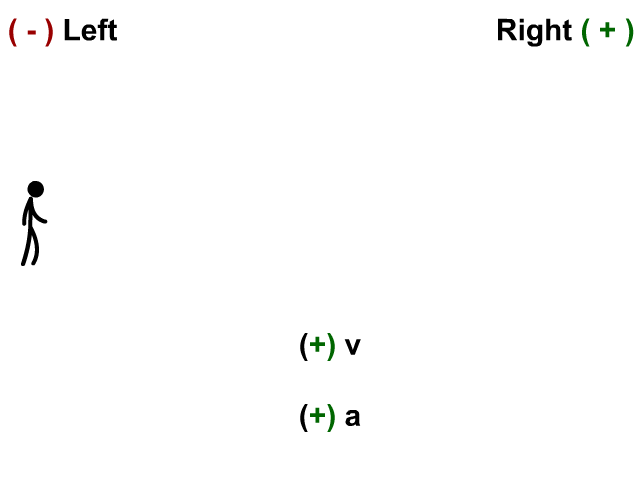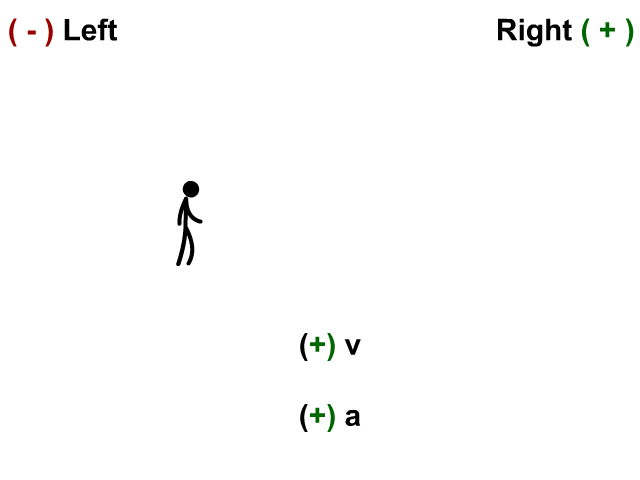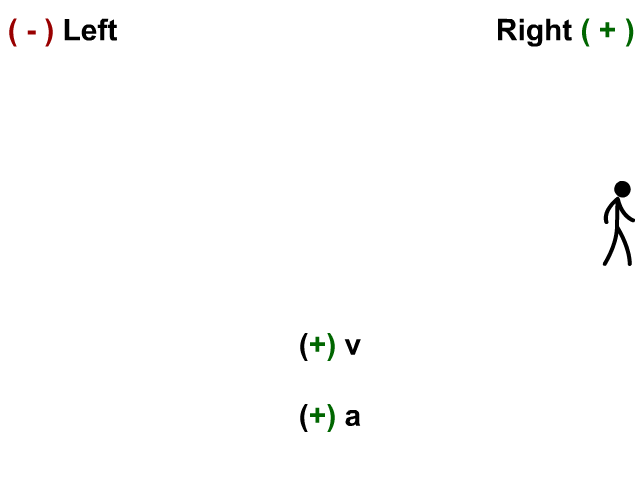
Velocity and Acceleration Positive
Here the stickman has a velocity to the right and his acceleration (velocity is changing) to the right.
- When v and a are positive you have acceleration
Velocity Positive and Acceleration Negative
Here the stickman has a velocity to the right and his acceleration (velocity is changing) to the left.
- When v is positive and a is negative you have deceleration
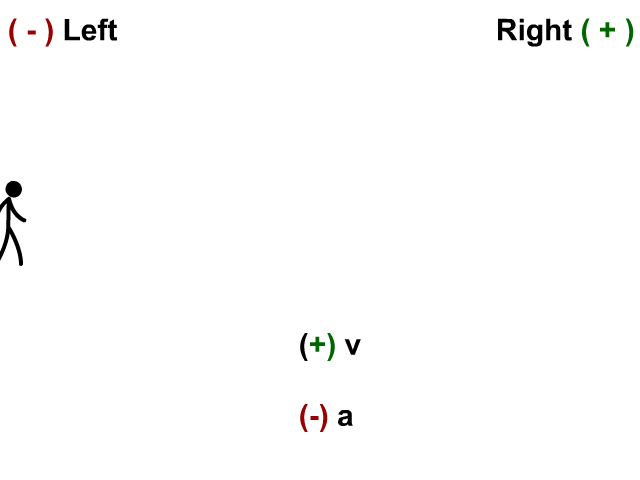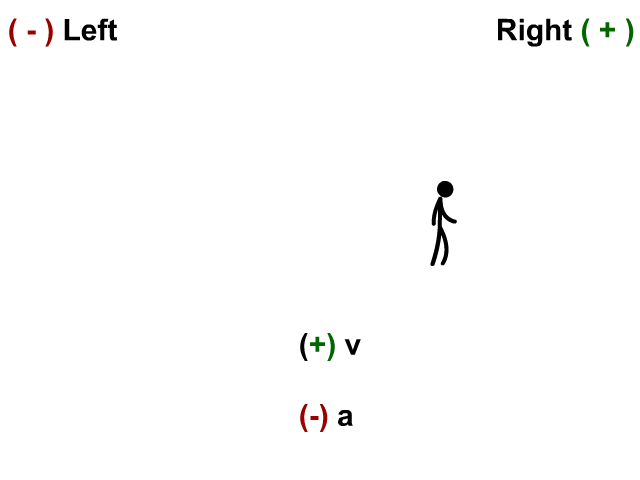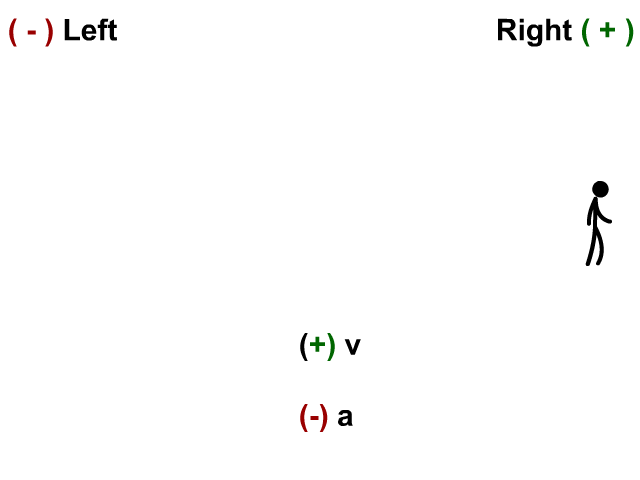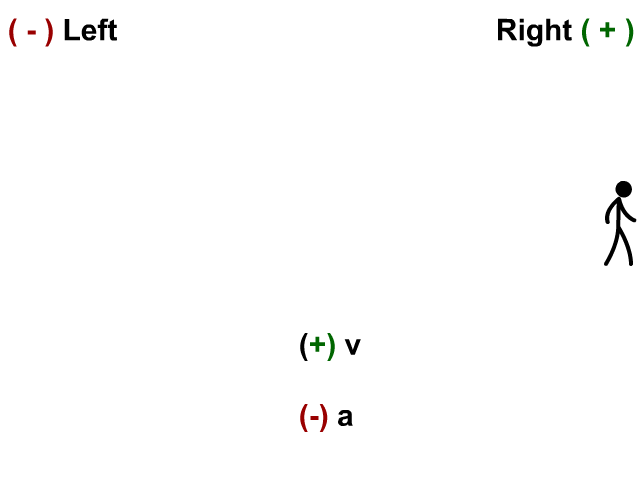
Velocity Negative and Acceleration Positive
Here the stickman has a velocity to the left and his acceleration (velocity is changing) to the right.
- When v is negative and a is positive you have deceleration
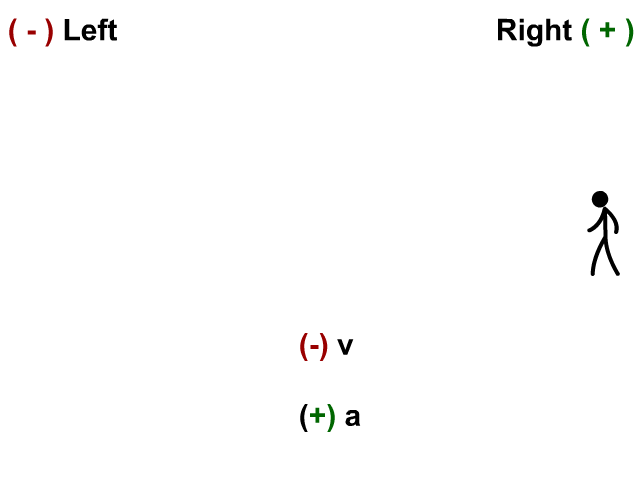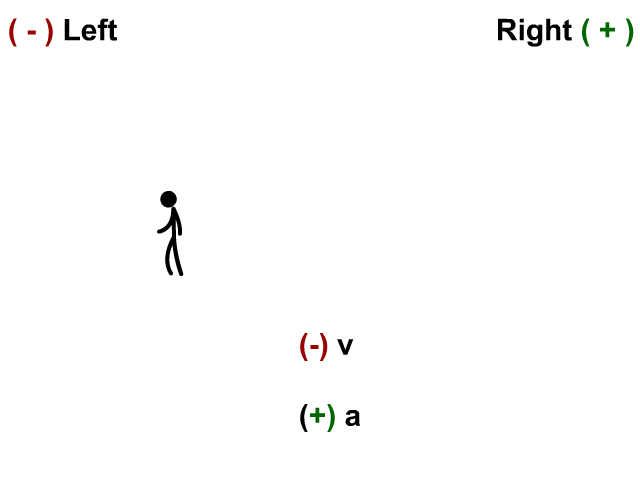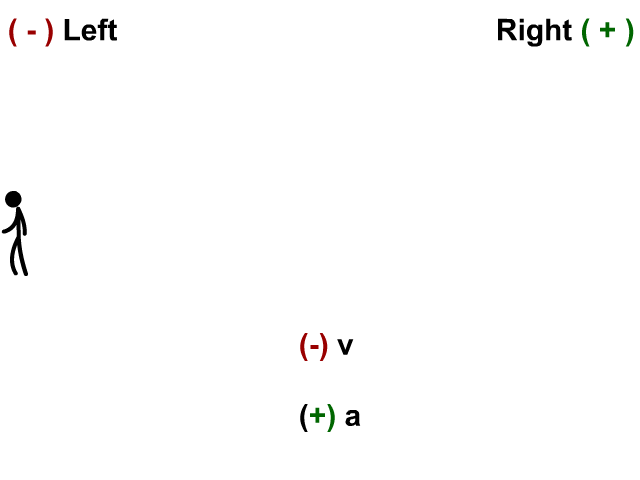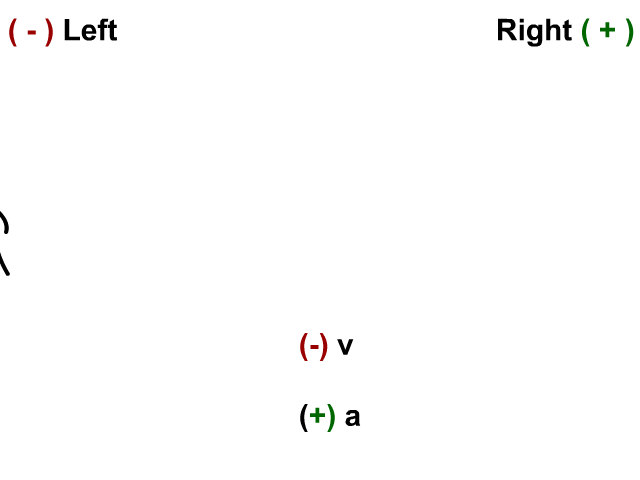
Velocity and Acceleration Negative
Here the stickman has a velocity to the left and his acceleration (velocity is changing) to the left.
- When v and a are negative you have acceleration

Note:
- When the direction signs for velocity and acceleration are the same you accelerate
- When the direction signs for velocity and acceleration are opposite you decelerate

Q3: In which motion is the direction sign for velocity negative but acceleration positive?
Q4: What would you call motion that has the sign for velocity negative but acceleration positive?
Comparing Acceleration, Velocity, and Displacement
- Acceleration is how much velocity is changing in a direction
- Velocity is how fast you are moving in a direction
- Displacement is how far you traveled in a direction
- Time is how long it took
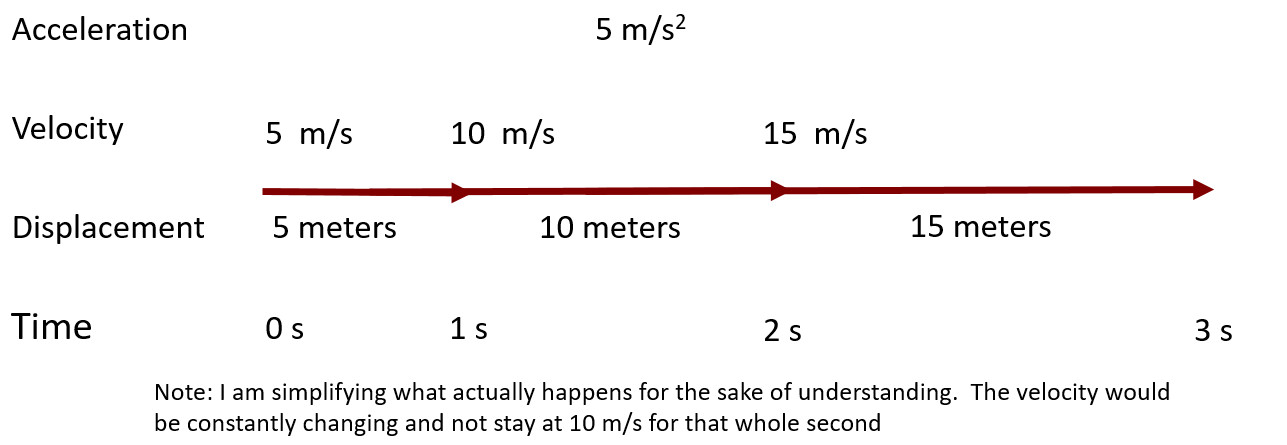
Acceleration Equation Variables
| Name | Variable | Unit | Unit Abbreviation |
| Initial Velocity or Initial Speed | vi | meters per second | m/s |
| Final Velocity or Final Speed | vf | meters per second | m/s |
| Time | t | seconds | s |
| Acceleration | a | meters per second squared | m/s2 |
| Displacement or Distance | X | meters | m |
Most Common Acceleration Equation
The most common acceleration equation is it's definition. Acceleration equals change in velocity over time.
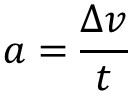
With change in velocity expanded out below:
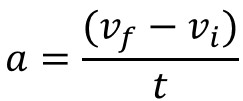
The following acceleration equations can be used to answer any accelerated motion problems. Observe the variables in our animated videos.
Q5: A car accelerates from a traffic light and increases its velocity from 0 m/s to 20 m/s in 5 s. What is its acceleration?
Acceleration Equations and Picking the Right One For Your Problem
Notice there are five total variables in these equations
vi vf a x t
You can solve any problem that gives you three knowns and one unknown you are asked for.
Make a givens list to help you choose the only one equation that has your three knowns and one unknown
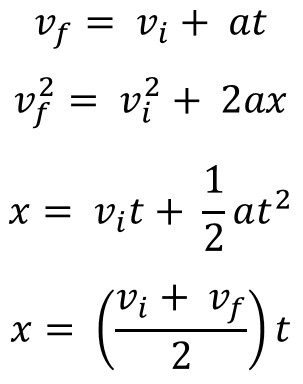
Example: What is the initial velocity of a train that takes 30 m to get to 15 m/s from at a rate of 2 m/s2?
Notice how important it is to have all the givens including the unknown written on your paper before you choose the equation. Only one equation can be used because you know nothing about time.
- Its what you don't know and are not asked about that helps you pick the right equation.
- Ocassionally when you have additional information, for example four knowns and one unknown, you can pick multiple equations to use If you do the math right, both will give you the same answer.
Givens
vi = ?
x = 30 m
vf = 15 m/s
a = 2 m/s2
notice you are not asked or have any information about t (time).

Then we do the work.
Notice, you will not always be solving for the variable to the left of the equals sign.
You will often have to rearrange the equations a bit before you solve. Some students like to plug in values and minimize the algebra before solving which is fine as long as your teacher says so.
Quick note before you get some acceleration equation practice
if you are not told that there is a slowing down or a speeding up or the problem says constant velocity, a= 0 m/s2 and you use the constant or average velocity equation v=x/t.
Watch out for key words in word problems
Q6. What does the following tell us about certain variables or ask for?
A) How fast was it going?
B) How fast will it go?
C) Object starts from rest
D) Object slows down
E) Object comes to a stop
F) At a constant velocity
Observe the videos below to see the variables from our acceleration equation in action
vf = vi + at
Final velocity equals the initial velocity plus the acceleration times the time. Common version of this equation can be seen below.
x = vit + ½ at2
Displacement equals initial velocity times time plus one half acceleration times time squared.
vf2=vi2 + 2ax
Final velocity squared equals initial velocity squared plus two times acceleration times displacement.
x = ((vi + vf)/2)t
Displacement equals the sum of initial velocity and final velocity divided by two and then multiplied by time
Picking your acceleration equation
Once you determine an object is speeding up or slowing down in a problem and you are given three variables and one to solve for, you know you have to pick from the acceleration equations.

Steps to Working an Acceleration Problem Correctly
Example question as you walk through the steps. How fast was Chancellor running after starting from rest and accelerating at 4.5 m/s2 for 2 seconds?
- Step one: read the entire problem
- Step two: pick out the unknown the question is asking you to solve for and add it to a givens list. (example: vf = ?)
- Step three: pick out the variables given in the equation. (example: vi = 0 m/s, a= 4.5 m/s2, t= 2s)
- Step four: figure out which variable is missing (example: x is missing)
- Step five: pick the one equation that does not have that missing variable (in this example: vf = vi + at)
Example Problems
1. How fast is Tommy Running after starting from rest and accelerating at 2 m/s2 for three seconds?
2. A car travels for 10 seconds at a constant velocity of 20 m/s. What is its acceleration over that ten second period?
3. How much time would it take to go from 10 m/s to 35 m/s in 50 meters?
4. How much did you accelerate when starting from rest and traveling 230 meters in 15 seconds?
5. How far would you have traveled after starting from 2 m/s and speeding up to 12 m/s at 3 m/s2?
Links
- Continue to Physics Motion Graphs
- Back to the Stickman Physics Home Page
- Find many of your animation resources in one place at the StickMan Physics Gallery
- Equation Sheet