Scalars and Vectors
Learn the difference when describing and using scalars and vectors. See how to use the scalars distance and speed and vectors displacement and velocity mathematically.
Optional: Buy a guided set of notes for this page at Teachers Pay Teachers if your teacher has not provided one.
Scalar and Vector Learning Targets
- I know the variable and unit for velocity, time, and displacement
- I understand the difference between scalars and vectors
- I can calculate the distance and displacement of an object that moves along a straight line path
- I can calculate the speed and velocity of an object that moves along a straight line path
- I know the difference between instantaneous velocity and average velocity of an object
- I understand how acceleration is different than velocity
Physics is a math based science used to explain and predict natural phenomenon in the world around you. We will begin our lessons with Kinematics, the study of motion.
Physics Variables and Equations
We use equations to answer questions using measured variables in an experiment or given variables in a question. It is important to know the variables your class uses and units which will help you determine equations to use. While the physics stays the same, a different textbook may use two different letters to represent variables of the same equation.
For example displacement may be represented by the variable d in one book or X in others. We will be using X for displacement on our pages. The first equation we'll use is velocity equals displacement divided by time. This is represented by the equation v=X/t. This would be the same as v = d/t if your teacher used d to represent displacement.
Basic Velocity and Speed Variables
| Name | Variable | Unit | Unit Abbreviation |
| Displacement or Distance | X | Meters | m |
| Time | t | Second | s |
| Velocity or Speed | v | Meters Per Second | m/s |
| Acceleration | a | Meters Per Second Per Second | m/s2 |
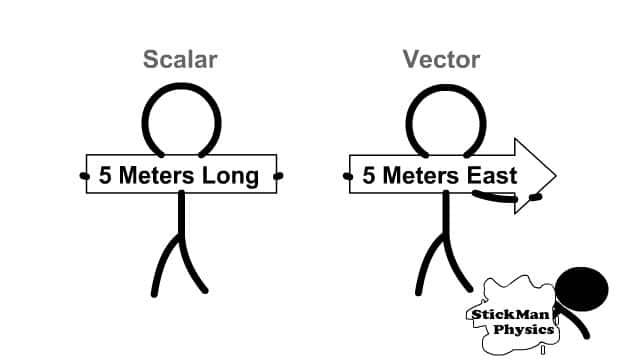
How are scalars different than vectors?
A scalar in physics includes only a magnitude. A magnitude is a number and a unit. Two common scalars are distance, for example 5 meters, and speed, for example 5 meters per second. Speed is a scalar because it uses the scalar distance traveled per time.
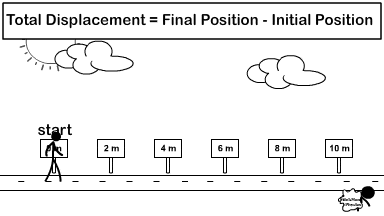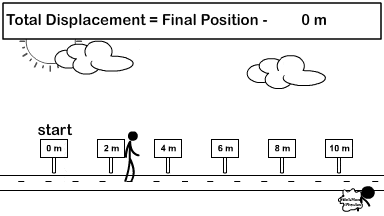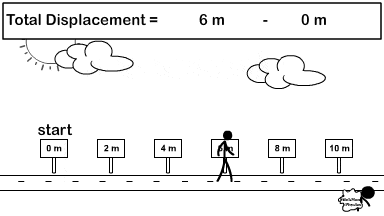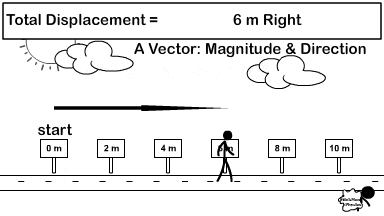
A vector in physics includes a magnitude and a direction. Two common vectors are displacement like 5 meters east and velocity like 5 meters per second east.
How is distance different than displacement?
Distance (a scalar) is a measure between two points. Because distance has no direction you add up all of the segments traveled.
Displacement (a vector) is a measure of where you are from the origin, or starting point, and in what direction.
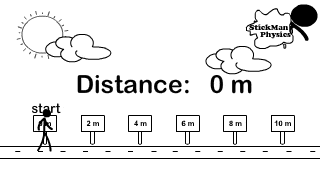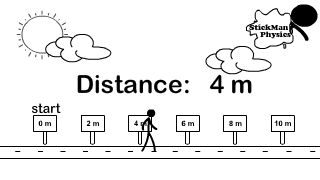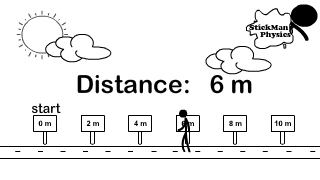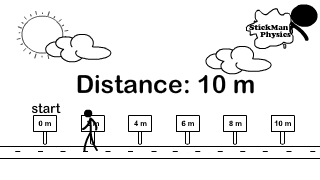
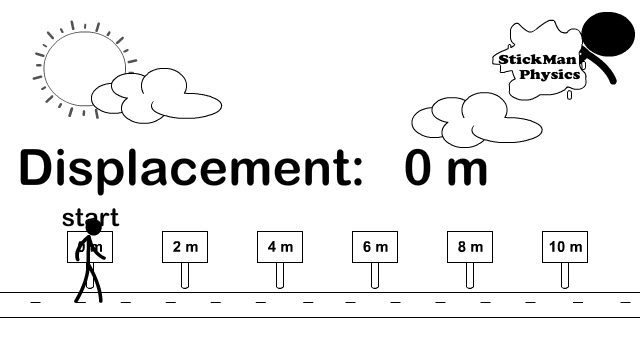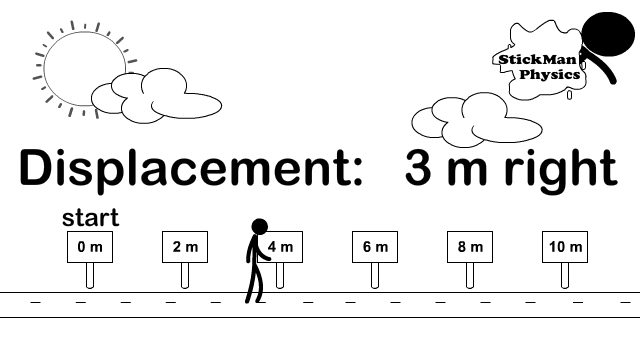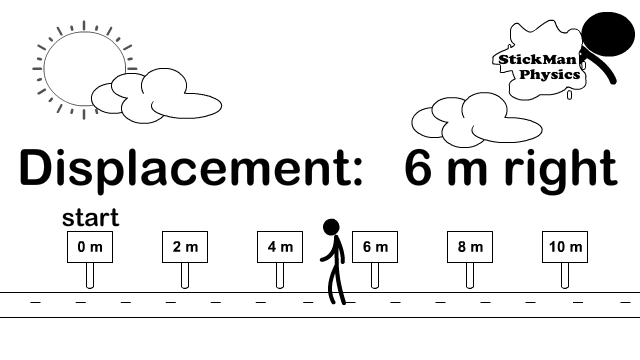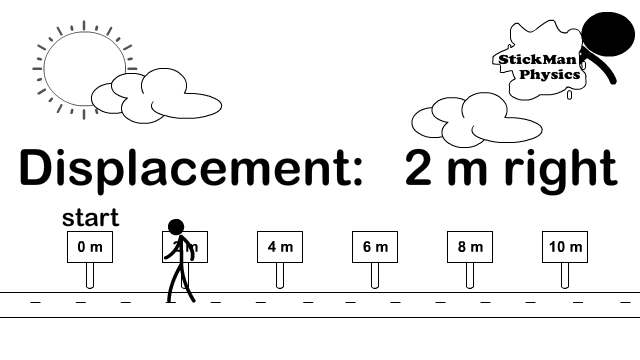
Scalar Distance and Vector Displacement
How do you calculate distance and displacement?
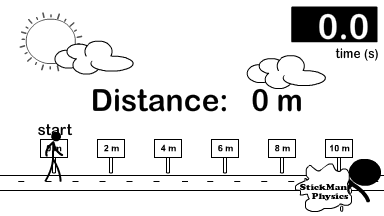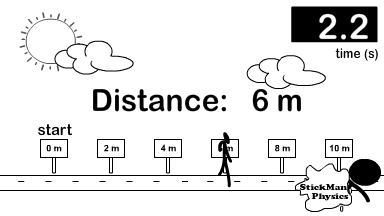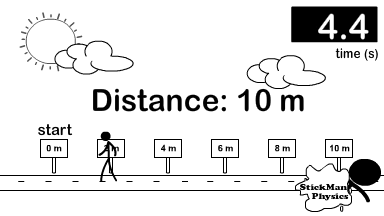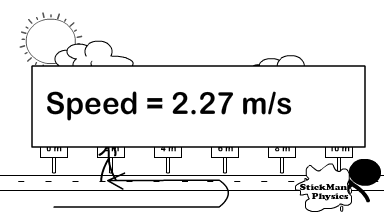
Look at the difference between how distance and displacement are calculated. The stickman in the picture goes right from the origin (0 meters) all the way to 6 meters. Then he turns left and travels 4 meters back. Because direction does not matter, for distance you add every meter traveled in any direction up. So 6 meters + 4 meters.
Distance = 6 + 4 = 10 meters
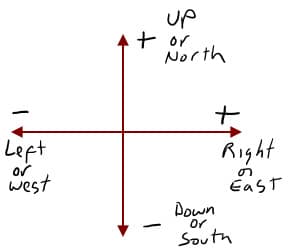
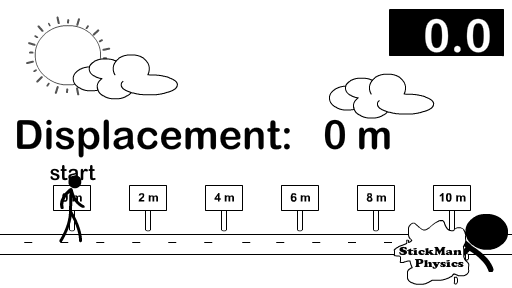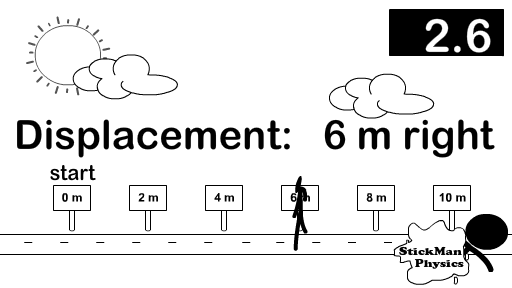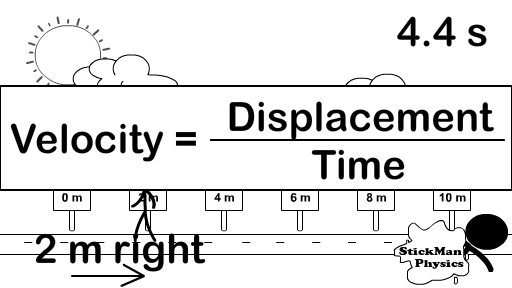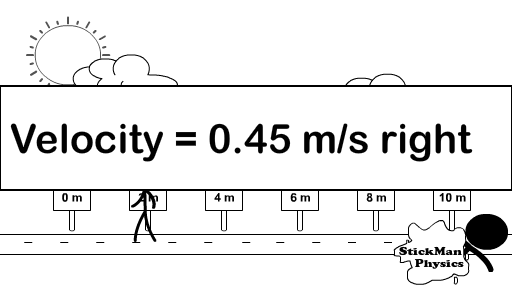
For the displacement vector you turn direction into a mathematical sign and add vectors. Observe the picture to the right showing common signs to replace directions. So we call right positive and left negative. Therefore 6 meters right becomes +6 meters and 4 meters left becomes -4 meters. Now add the vectors but include the signs (+6) + (-4) = +2.
Displacement = (+6) + (-4) = +2.
Once you have your final answer turn the sign back into a direction and then include the unit. So +2 becomes 2 meters right.

Calculating Scalar Speed and Vector Velocity
Scalars go with scalars, so use distance to calculate speed as seen in the equation on the right.
Vectors go with vectors, so use displacement to calculate velocity as seen in the equation to the right.
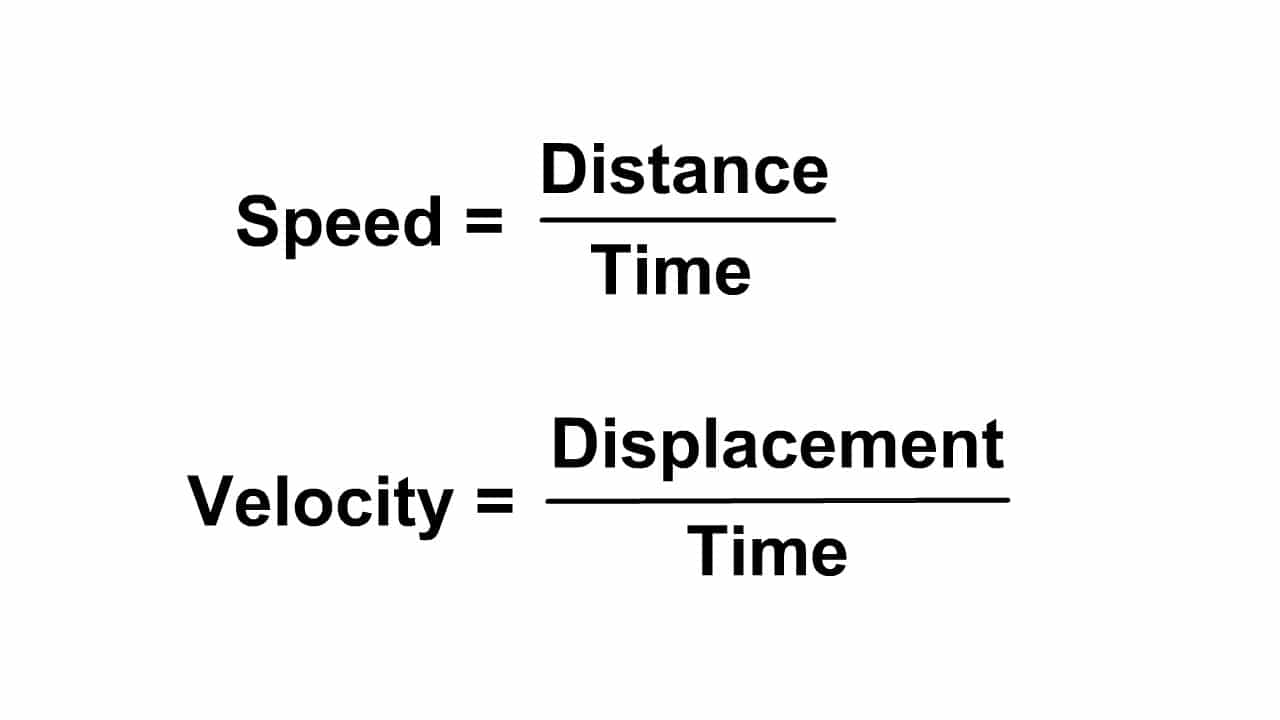

The equation in the animation to right (v =Δx/t and also seen in two forms in the picture above it) will be used in examples to calculate speed or velocity but I will use distance if calculating speed and displacement if calculating velocity.
- In different equations x or Δx may be used interchangeably to represent displacement or position.
- Δx would represent change in position (xf – xi) and displacement is often just written as x in common equations.
- A time interval (t) can be calculated (tf – ti)
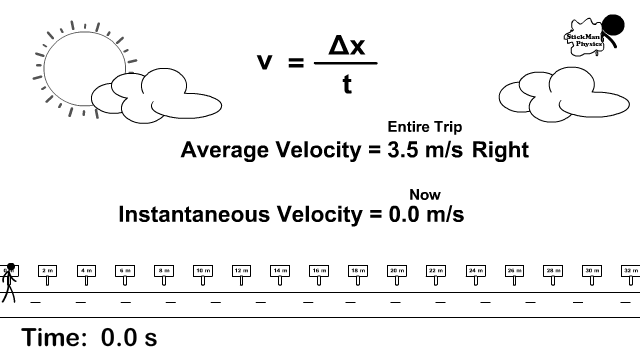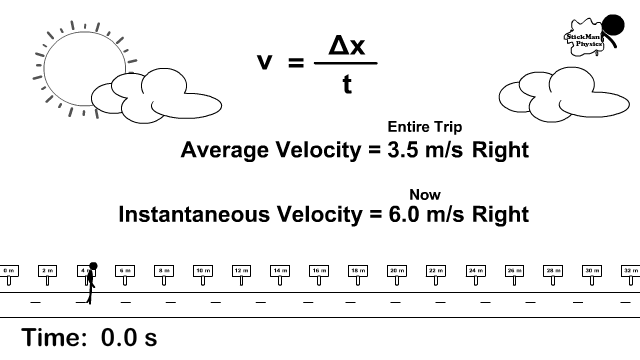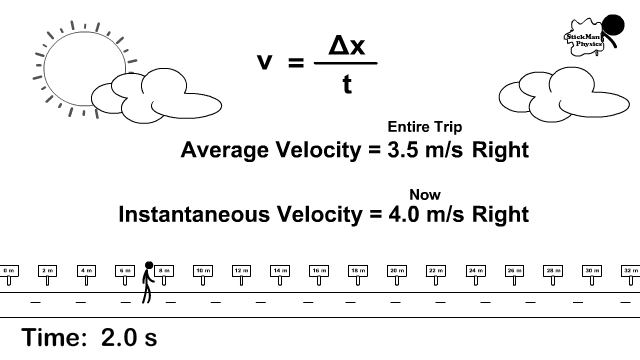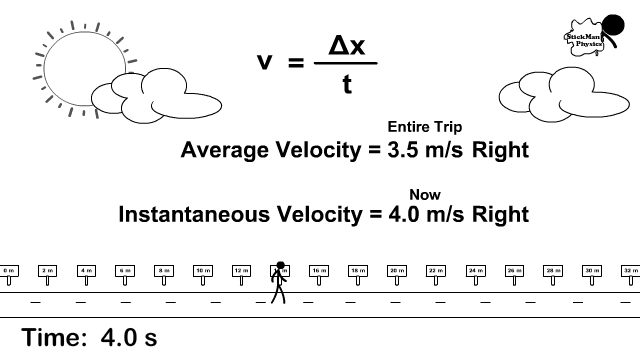
Notice in the picture to the right the stickman stops and goes at different rates.
How is instantaneous velocity different than average velocity?
- Instantaneous velocity is the velocity at that instant. For example, if stopped, his instantaneous velocity is 0 m/s but a few seconds later he is going again and its 4 m/s.
- Total displacement divided by the total time is average velocity. In the animation to the right, the total displacement was +14 m and the time it took was 4 seconds. v = +14/4 becomes 3.5 m/s forward.
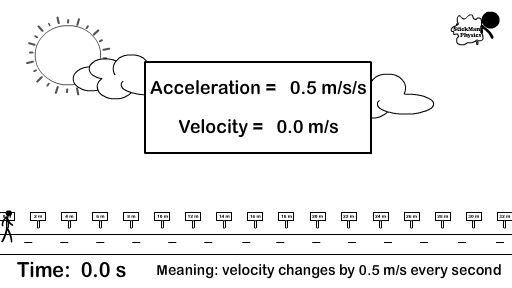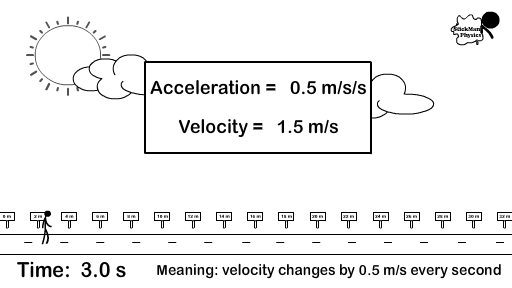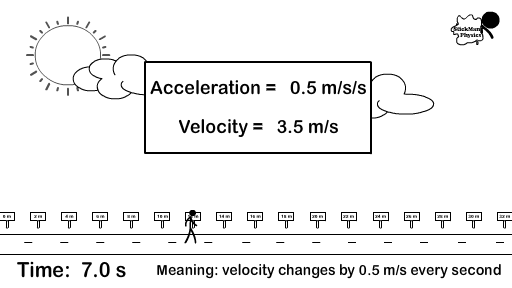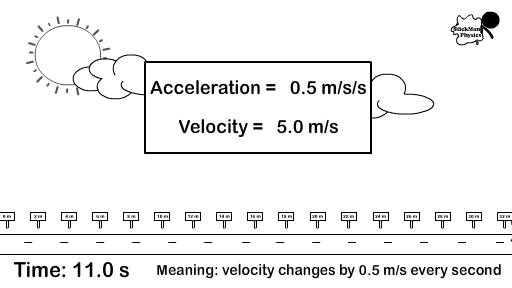
What does acceleration describe?
Velocity is how far you are traveling from starting point during a time period including the direction. If your velocity never changes you are traveling at a constant velocity.
Acceleration describes how velocity changes from an initial velocity during a time period. You can accelerate by going faster, going slower (also called deceleration), and changing directions.
Since acceleration describes a velocity change over time, the acceleration unit includes the unit for velocity (m/s) over another time period (s). Therefore, the unit for acceleration is m/s/s or more commonly m/s2. Acceleration is also a vector and would include the direction that the velocity is changing.
- A velocity of 5 m/s (meter per second) forward means that you travel five meters every second.
- After one second you are 5 meters forward. After two seconds you are another 5 meters forward (10 meters total).
- An acceleration of 5 m/s/s or 5 m/s2 (meters per second per second) forward means that you travel five meters per second faster every second. You would have to know your starting velocity to determine your ending velocity. Accelerating a 5 m/s2 means you are changing your velocity by five meters per second every second.
- If you started from rest (a velocity of 0 m/s) and accelerated at 5 m/s2, your velocity is 5 m/s after one second, 10 m/s after two seconds.
As we end this section is it important that you memorize your units. (Note cards are helpful)
- displacement and distance has the unit meter (m)
- velocity and speed has the unit meters per second (m/s)
- time has the unit seconds (s)
- acceleration has the unit meters per second per second which is the same as meters per second squared (m/s/s or m/s2)
You'll learn various means to calculate acceleration in the next section of this unit. Before we go there, lets look at how to calculate using scalars and vectors.
Observe the animations below to see how displacement and distance are measured. Then observe how the vector velocity uses displacement in its calculation while the scalar speed uses distance. If an object never changed directions, the magnitude for velocity and speed would be the same.
What is happening to the displacement after the stickman reverses direction and continues moving?

What is happening to the distance traveled after the stickman reverses direction and continues moving?

Solving for other than v using the constant velocity equation
How much time does it take to go 500 meters at a speed of 20 m/s?
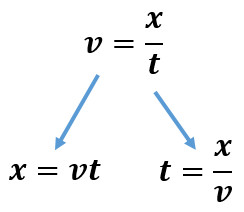
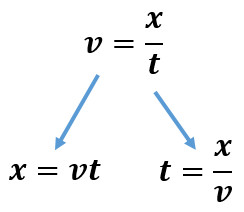
Scalar Vector Example 1
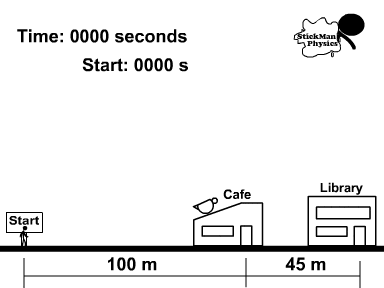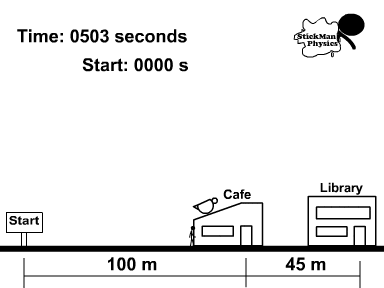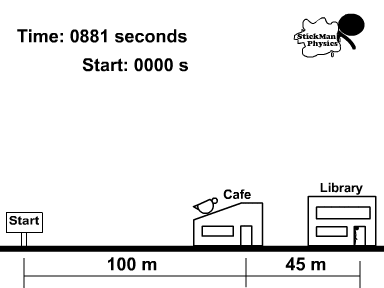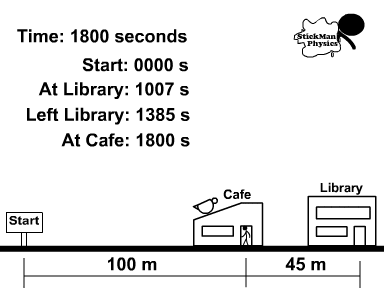
Use the picture to the right for the following questions.
Thomas, on his lunch break, took 30 minutes to go to the library and then the cafe.
1. What distance did Thomas travel during lunch?
2. What was his displacement?
3. Determine the speed of Thomas during the 30 minute (1800 second) lunch?
4. What was the velocity of Thomas during the 30 minutes?

Links
- Continue to part 2: Accelerated Motion and Equations
- Go to the 1D Motion Unit Page
- Back to the Stickman Physics Home Page
- Equation Sheet