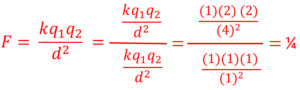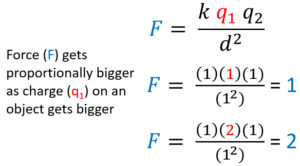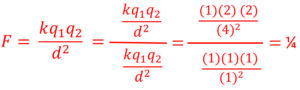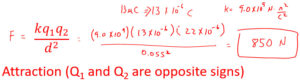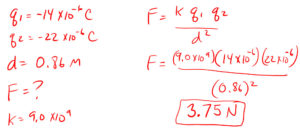Coulomb's Law: Calculating the Electrostatic Force

Learn about Coulomb's Law and electrostatic or electric force. The attractions or repulsion caused by two charges being a distance from each other.

Newton's Third Law and Electrostatic Force

Coulomb's Law Learning Targets

I can relate Newton’s Third Law of motion to charges
I understand Coulombs law and relationship between electrostatic force, charge, and distance
I can solve for electrostatic force, charge, and distance using Coulomb’s Law with two charges

Watch a video lesson about Coulomb's Law and the electrostatic force or go below and read and work through samples at your own pace like a textbook.

Coulomb’s Law Variables
Name	Variable	MKS Unit	Unit Abbreviation
Force	F	Newton	N
Coulomb’s Law Constant	k	Newton meter squared divided by Coulomb squared	Nm²/C²
Charge(s)	q, q₁, or q₂	Coulomb	C
Distance	d	Meters	m
Radius	r	Meter	m

Electrostatic Charge (q)

The MKS standard physics unit for charge (variable q or Q) is the coulomb (C). Note: depending on your equation sheet you may use the variable q or Q. We will use q to represent charge in this unit.

One Coulomb is equal to the charge of 6.25 x 10¹⁸electrons. This is beyond what you'd normally encounter unless calculating charge carried in a lightning strike. Since a coulomb is such a large charge, the prefix micro (µ) or 1x10^-6is often used to describe a charge. If you see the unit µC, just add (x10^-6) to your number to make it Coulombs when solving equations. So, 5 µC would be equal to 5x10^-6C.

What Are Three Factors Affecting Electrostatic Force?

Three factors affecting electrostatic force are charge, the distance between the objects, and the insulating material between the objects. The problems from this section will all have charges separated by air as the insulator. All three factors above can be seen in the electrostatic force equation formally called Coulomb's Law.

Coulomb's Law And The Electrostatic Force

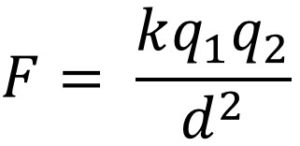
In the coulomb's law equation q₁and q₂are two charges. The force created (F) is dependent on the distance between the object (d) and the Coulomb's Law constant (k) for the insulating material that separates those charges. The Coulomb's Law constant for air is 9.0x10⁹ (Nm²/C²). Don't be intimidated by the unit (Nm²/C²) as only 9.0x10⁹ would be used in calculations.

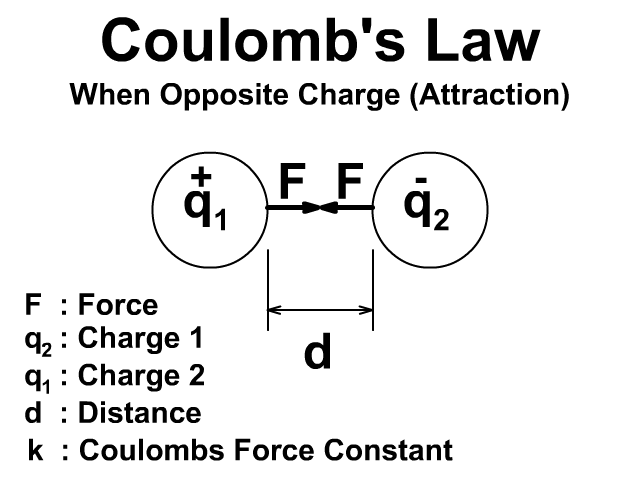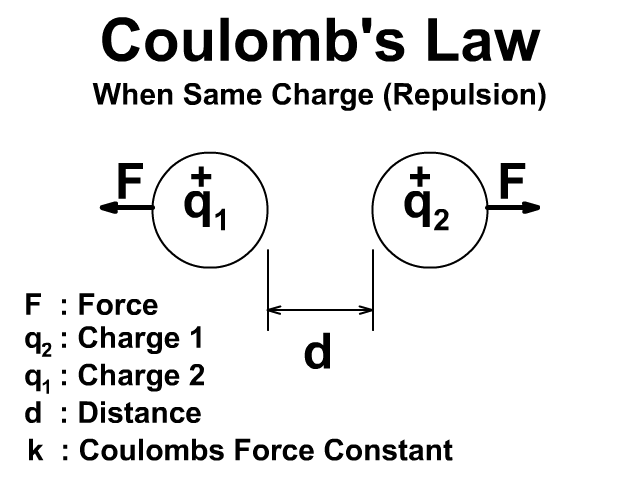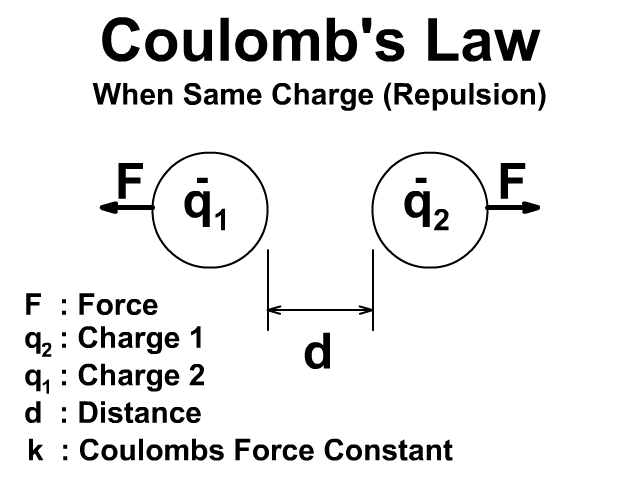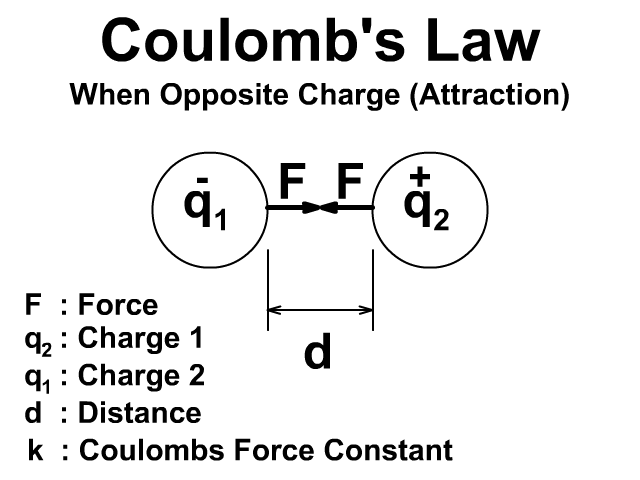
There will be an attractive force when the charges have opposite signs positive (+) and negative (-).

There will be a repulsive force when the charges have the same sign positive (+) and positive (+) or negative (-) and negative (-).

Either way the force is created in pairs on each object and that force is equal and opposite. To learn more about Newton's Third Law and action reaction pairs go back to that lesson here.

Electrostatic Force and Charge are Directly Proportional

Electrostatic force (F) and charge (either q) are directly proportional. To analyze this increase what you are analyzing,one charge (q₁), and see what happens to force when everything including one charge is 1. Afterwards make that charge 2 and see how force (F) increases at the same rate and becomes 2.

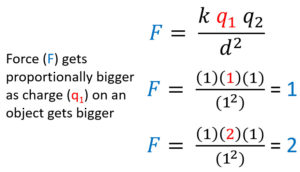
Electrostatic Force is Proportional to the Inverse Square of Distance

Electrostatic force (F) is inversely proportional to the inverse square of distance. As distance increases using the same method as before the force decreases proportional to the inverse squared. If distance goes from a 1 to a 2 the force goes from 1 to 1/4. Distance has a much greater effect on force that an equal increase or decrease of charge.

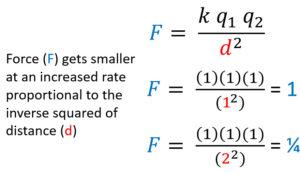
Rule of Ones and Coulomb's Law

To find the exact change in one variable to another you can use the rule of ones. Go back to that lesson by clicking the link if you are familiar with this method.

The Standard Type of Coulomb's Law Problem

Most Coulomb's Law problems will involve charges, distances, and forces that result. A problem will give you enough information and you will have to solve for an unknown. When using coulombs law to solve problems it is customary to leave the sign off of the charge. If you have two like charges there will be a repulsion. If the charges are opposite positive (+) and negative (-) there will be an attraction.

When the two charges using Coulomb’s Law are the same, you can simplify the formula. Since the charges are the same substitute q in for both q₁ and q₂. Then simplify as seen below:

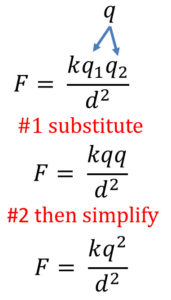
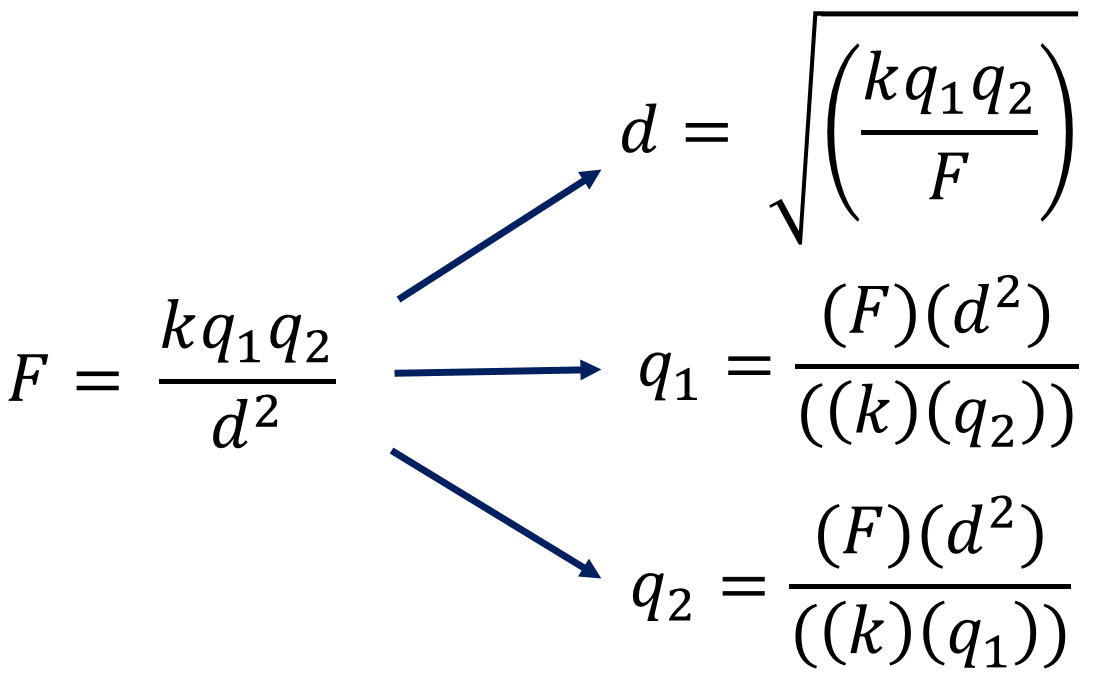
Coulomb's Law Equation and the Most Common Calculation Mistakes

You can see the end result of rearranging the Coulomb's Law equation for distance or either charge. I added extra parenthesis to help you avoid common mistakes.

The #1 Most Common Mistake Coulomb's Law Mistake: Solving for Distance Squared (d²) and Not Distance (d)

If a question asks you to solve for distance, you must take the square root of both d² and the other side of the equation. If not, you will be solving for d² accidentally when the equation asks for d. After taking the square root of both sides, d²will become d. You will also have a square root around the entire other side of the equation (kq₁q₂/F). When calculating, have an extra parenthesis around everything after square root. Doing this, √(kq₁q₂/F), will avoid accidentally taking the square root only a part of the side.

The #2 Most Common Coulomb's Law Mistake: k and q₂are not Included Together in the Denominator

If the question ask you to solve for either charge the rearranged equation involves the same algebra. Be sure to include extra parenthesis around the denominator, bottom of the equation as seen in the rearranged equation. This makes the calculator multiply the Coulomb's Law Constant (k) and the other charge (q₂) together in the denominator before doing anything else.

Example Problems

1. If the charge on each object is doubled and the distance between them is quadrupled, how will the force be affected?

(Click the picture to see a larger view of the work)

2. How are charge and electrical force proportional?

Directly: If a charge gets bigger, goes from 1 to 2, the force gets proportionally bigger, also goes from 1 to 2.

3. How is electrical force proportional to distance?

Proportional to the inverse squared of distance: When distance gets bigger, goes from 1 to 2, the force gets not just smaller but proportional to the inverse of distance squared. Force goes to 1/4. Distance has a greater effect on force than charge.

4. The better the insulator between the objects, the ______ the value of “k”.

Lower, if you had a better insulator the force felt between two charges would be less. So the lower the k the better the insulator. Once again, we are only doing math with air as the insulator and a k with a value of 9.0 x 10⁹Nm²/C²but this number would be less with a better insulator than air.

5. If the charge on each object is doubled and the distance between them is quadrupled, how will the force be affected?

6. What is the electrostatic force between two objects, +13 μC and -22 μC which are 0.055m apart (μC = 1 x 10^-6 C) and is it an attraction or repulsion?

(Click the picture to see a larger view of the work)

7. What is the electrostatic force between two objects of -14 x 10^-6 C and -22 x 10^-6 C that are 0.86 m apart?

(Click the picture to see a larger view of the work)

8. The electrostatic force between two objects is 6.4 N when the charges are -4.5 x 10^-6C and -8.8 x 10^-6C. How far apart are the objects?

(Click the picture to see a larger view of the work)

9. An attraction force of 1.1 N is exerted between two charged objects when they are 0.43 m apart. The charge on one object is -5.7 x 10 ^-6 C. What is the charge on the other object?

(Click the picture to see a larger view of the work)

Coulomb’s Law: Calculating the Electrostatic Force