Complex Circuits
Complex circuits have components that are in series and some that are in parallel. Lets start by reviewing series and parallel circuits and then see how a complex circuit works as a combination.
Series Circuits and Rules (Click Here to Go to the Lesson)
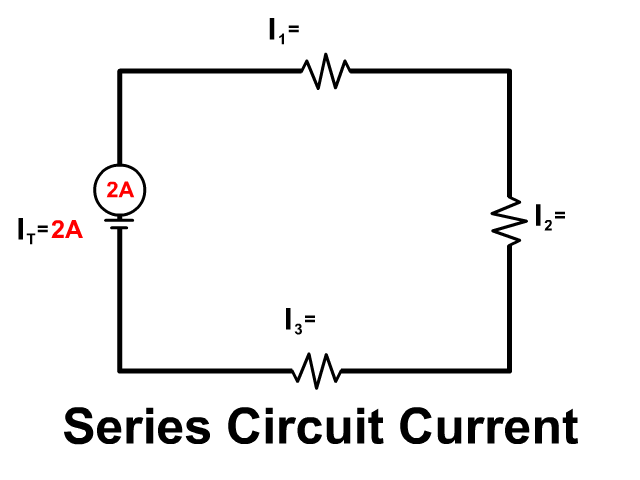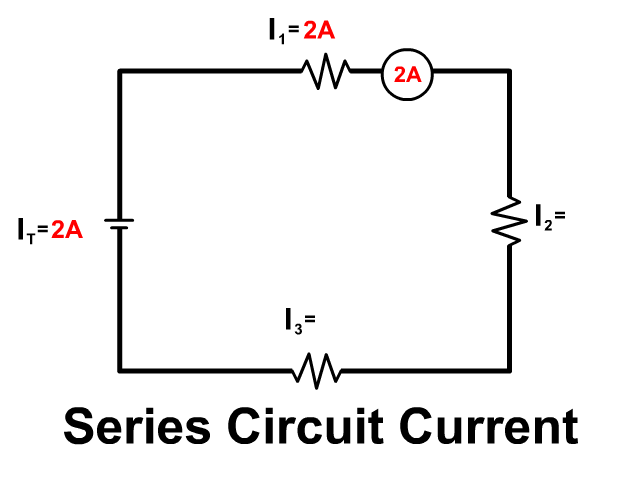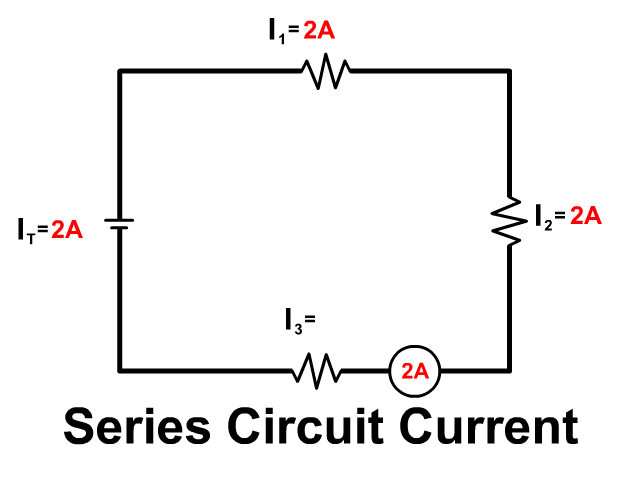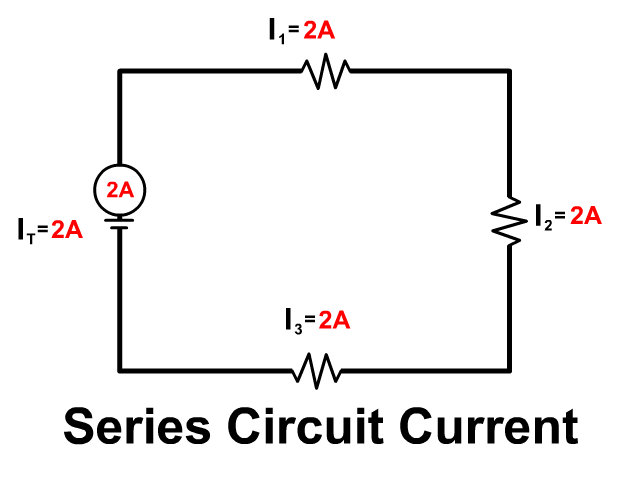
A series circuit you have no branches, current has only one path to follow. The same current remains together through all components from the positive terminal and back to the negative of the battery.
Ohm's Law (V=IR):
You can use this at a single location (T, 1, 2, 3, and any more) as seen below
- (VT) = (IT)(RT)
- (V1) = (I1)(R1)
- (V2) = (I2)(R2)
- (V3) = (I3)(R3)
Overall Series Circuit Rules
- VT = V1 + V2 + V3 + …
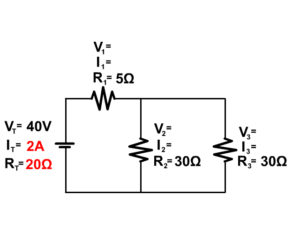
- IT = I1 = I2 = I3 = …
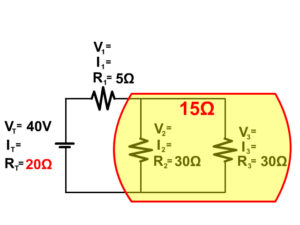
- RT = R1 + R2 + R3 + …
Parallel Circuit Rules (Click Here to Go to That Lesson)
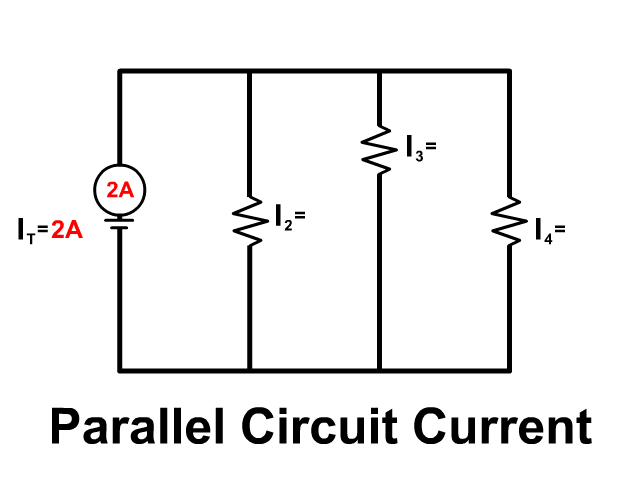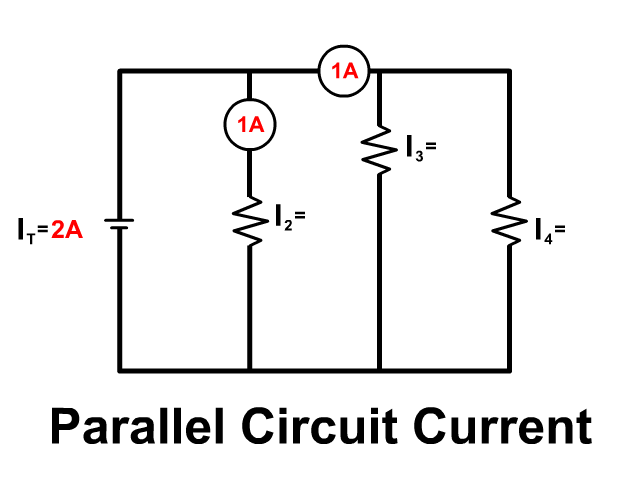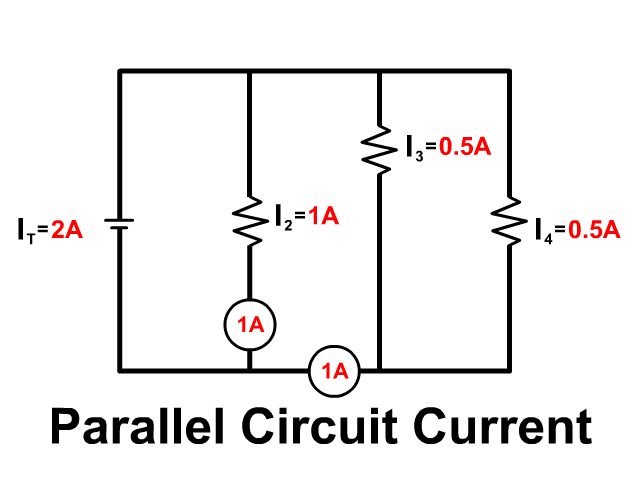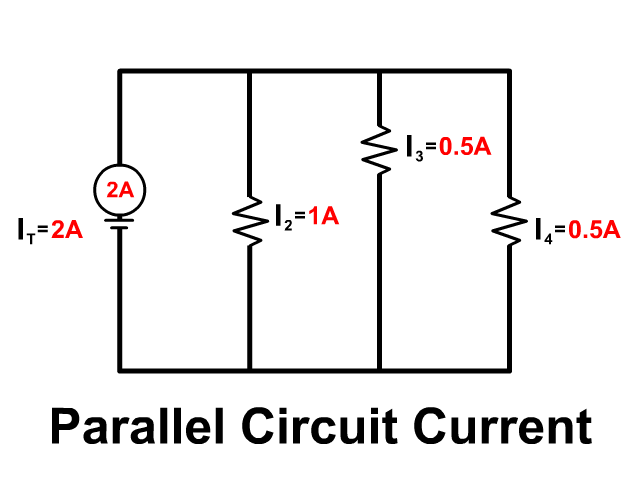
In a parallel circuit you have branches, multiple paths to follow. So current splits up but later comes back together as it returns to the battery.
You can use Ohm's Law (V=IR) at a single location the same as above in series circuits.
Overall Parallel Circuit Rules
- VT = V1 = V2 = V3 = …
- IT = I1 + I2 + I3 + …
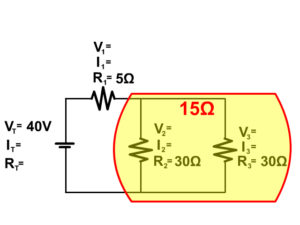
- 1/RT = 1/R1 + 1/R2 + 1/R3 + ...
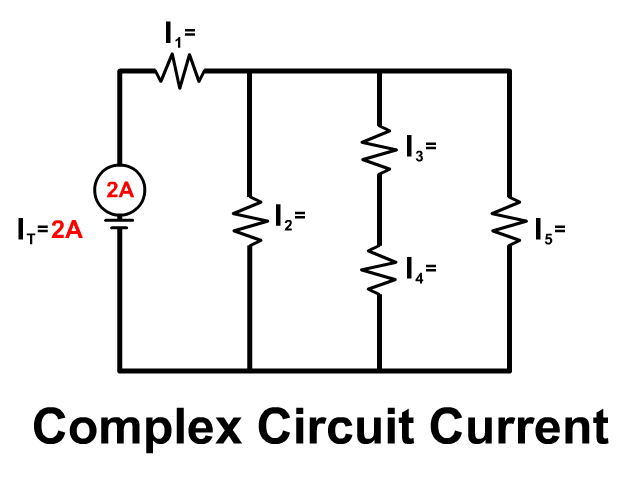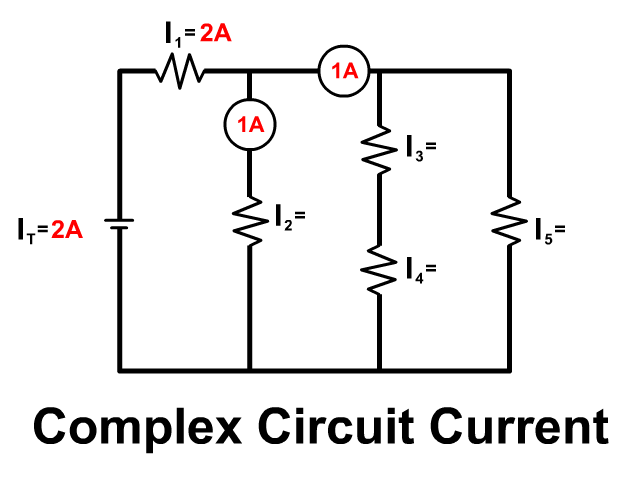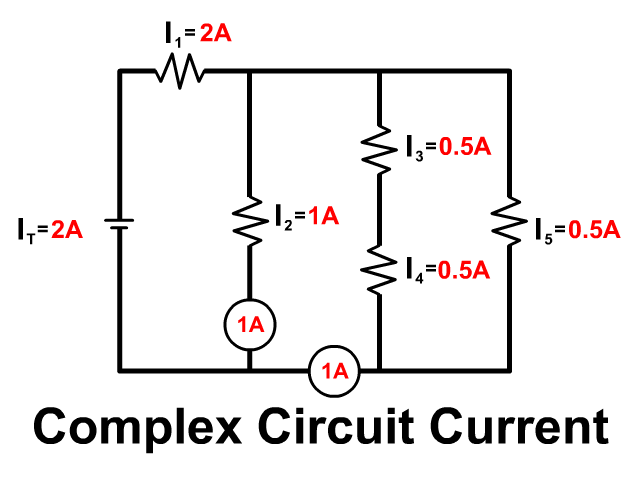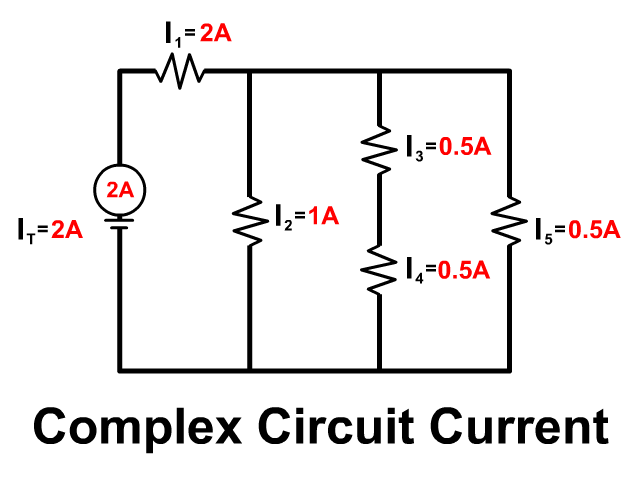
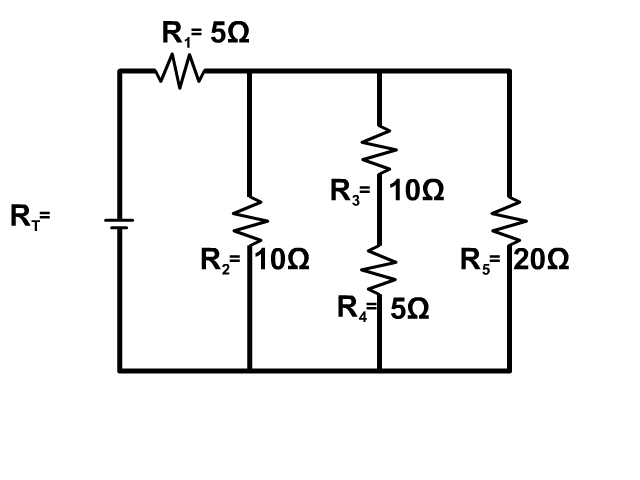
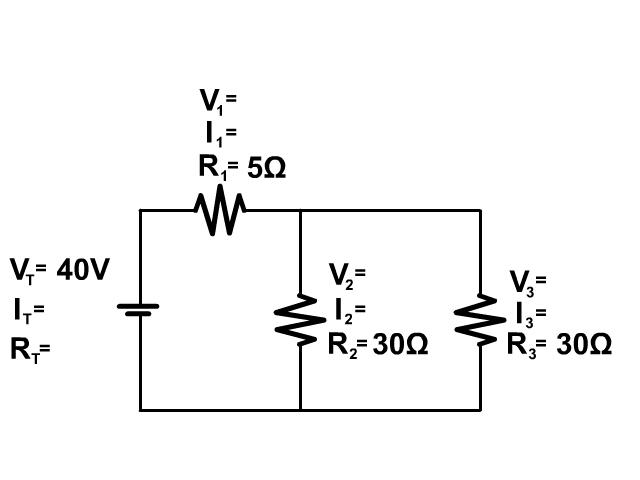
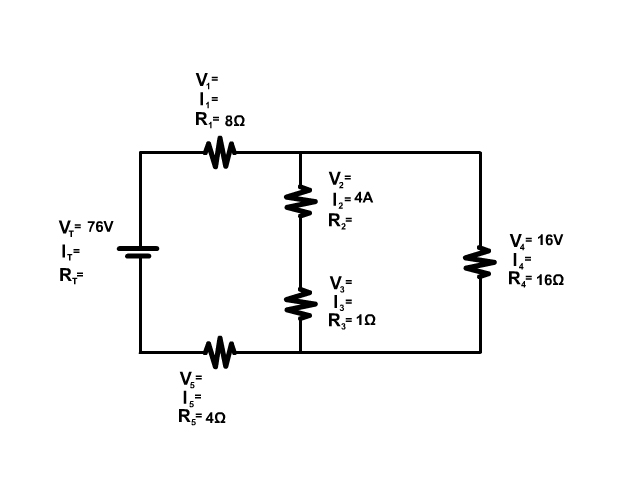
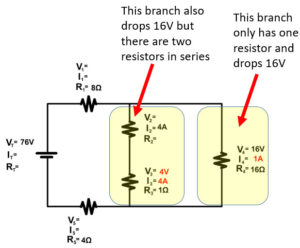
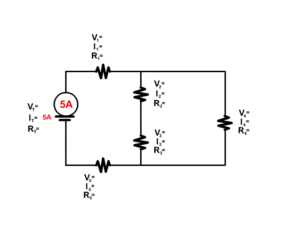
Complex Circuit
Follow the current from the positive terminal of the battery in the animation. Some parts of the circuit are in series and some in parallel.
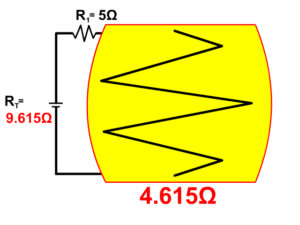
- The battery and resistor 1 are in series: 2A of current starts at the batter and flows through both.
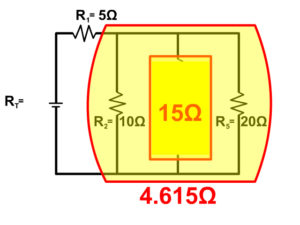
- The branch with resistor 2, the branch with Resistor 3 and 4, and the branch with Resistor 5 are in parallel: Current splits between these branches.
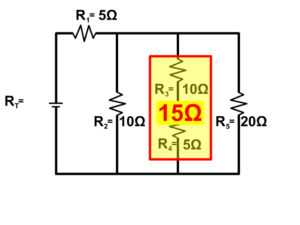
- The resistor 3 and resistor 4 are in series: Once current goes down the branch that same current must flow from both resistors.
Solving A Complex Circuit For Resistance
When solving for the resistance in a series circuit, the goal is to break down all the different parts making act like one single series circuit. Follow the steps or our example as we do this.
Example Problems
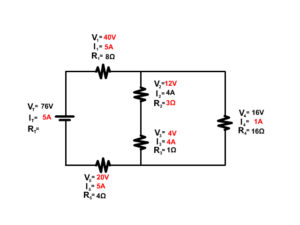
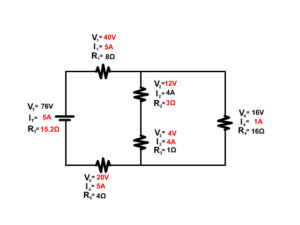
1. Solve for the total resistance of the complex circuit below.
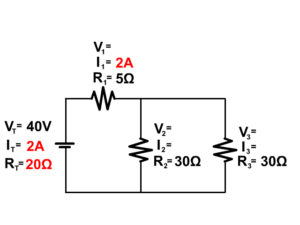
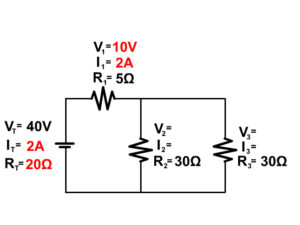
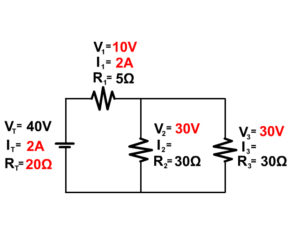
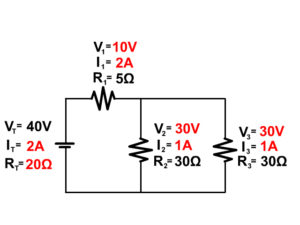
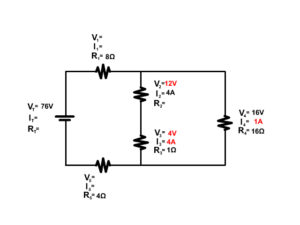
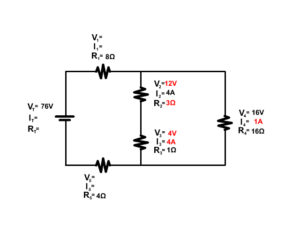
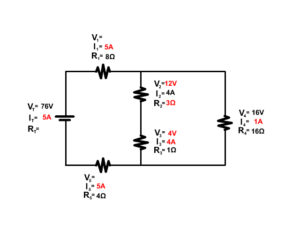
2. Solve for the unknown components of the following complex circuit.
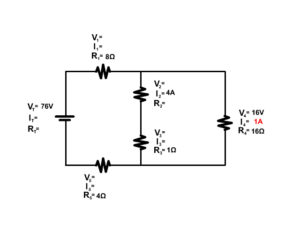
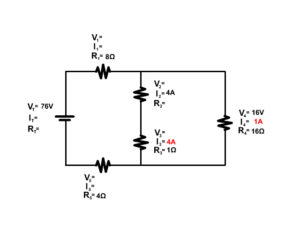
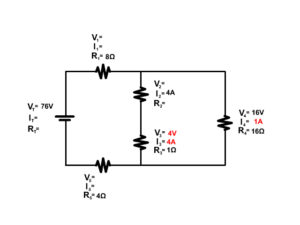
3. Solve for the unknown components of the following complex circuit.
Links
- Back to the Main Current and Circuits Page
- Back to the Stickman Physics Home Page
- Equation Sheet