Series Circuit

Home » Unit 8: Current and Circuits » Series Circuit

Series Circuits

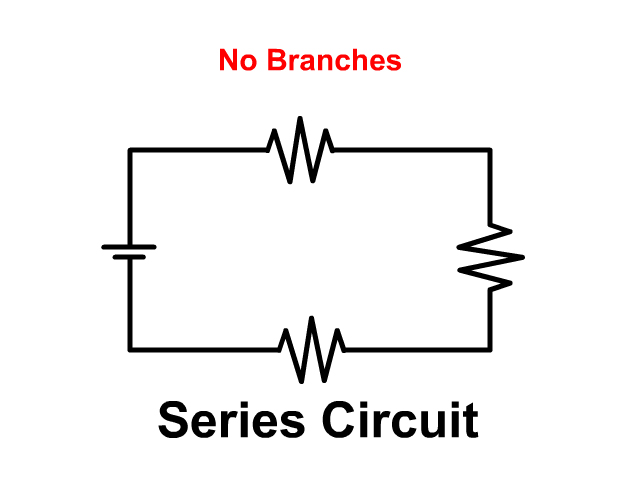
In a series circuit components like resistors and loads are connected in a single path.  Current must go through every component in order starting from the positive terminal of the battery through everything in order and back to the negative battery terminal.

Series Circuit Handout to go along with the problems on this page and the PhET lab at the end.

Basic circuit with three resistors and a battery in a series circuit

Series Circuits vs. Parallel Circuits

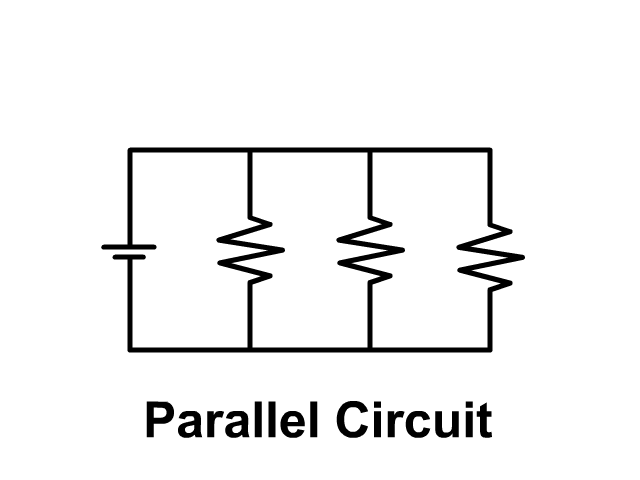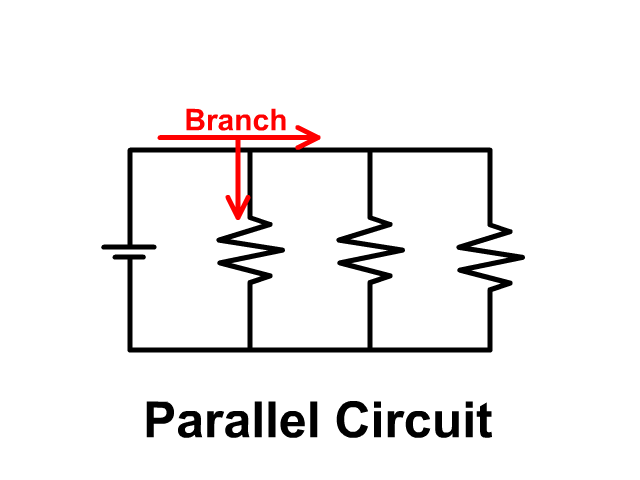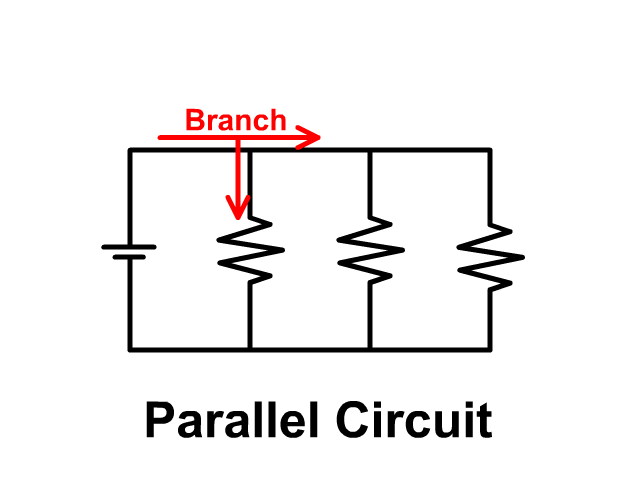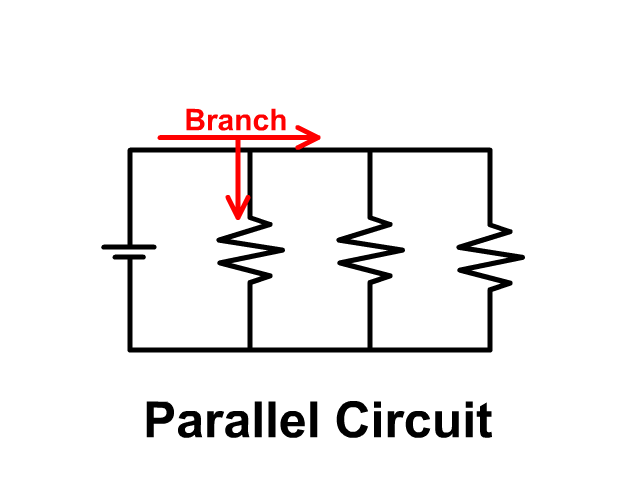
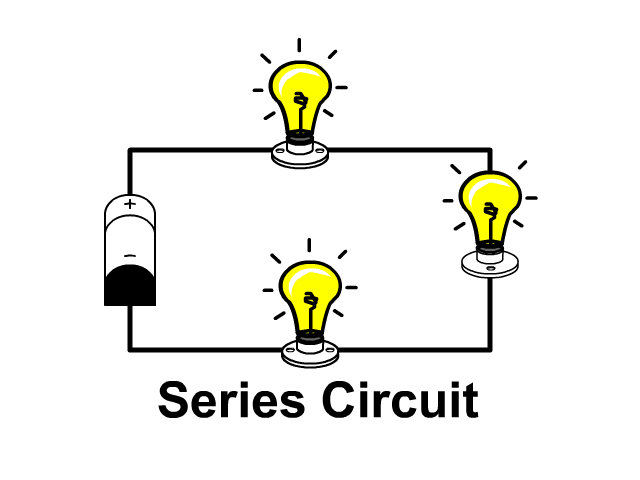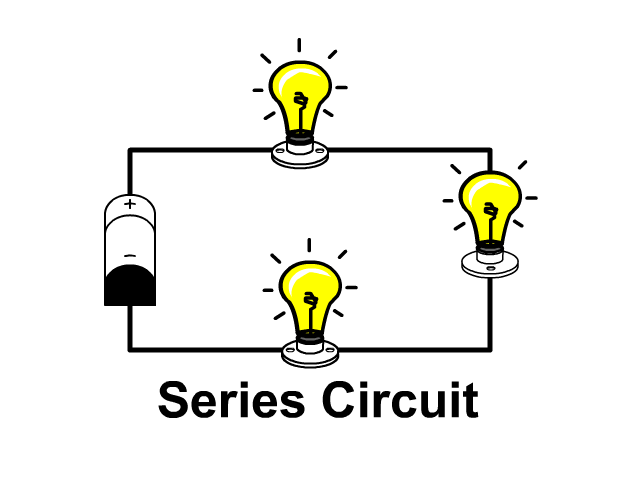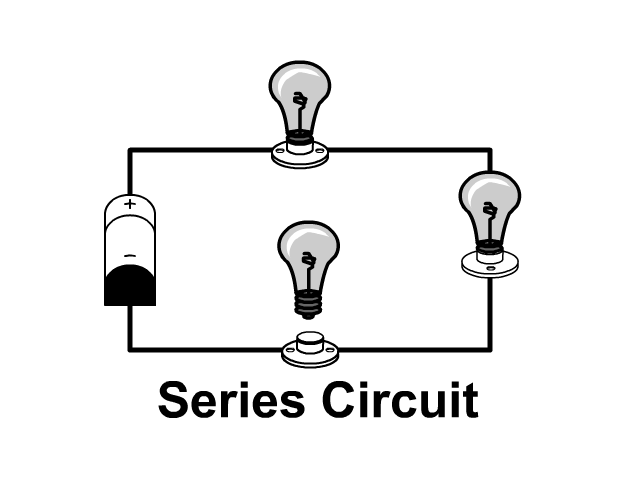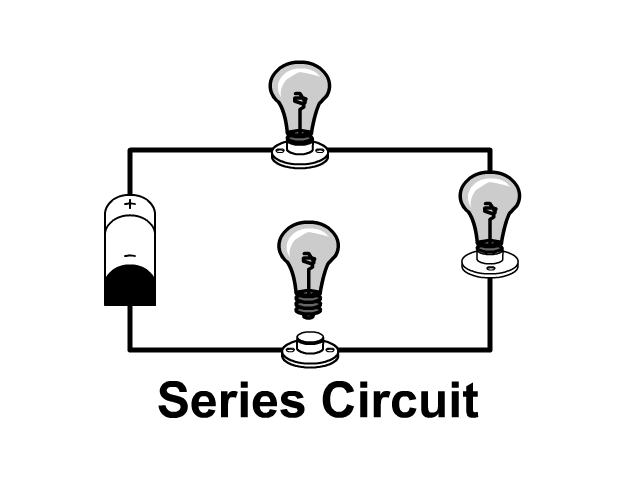
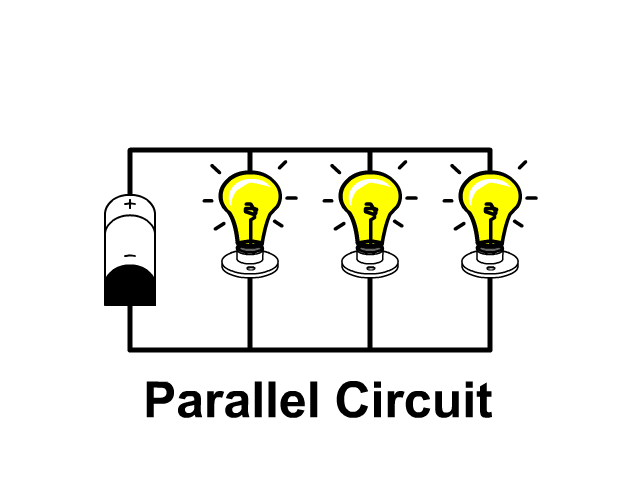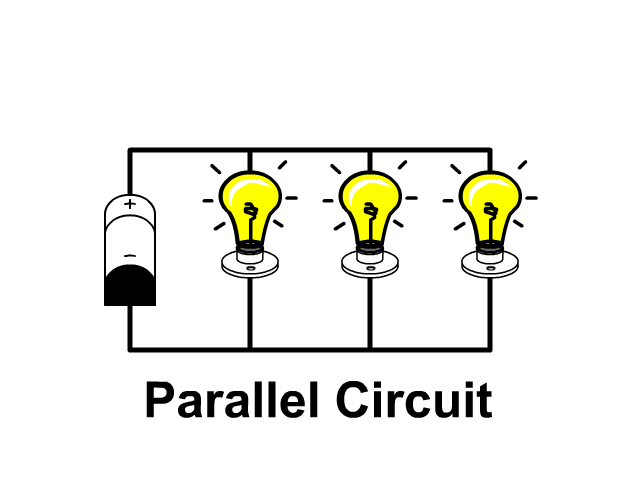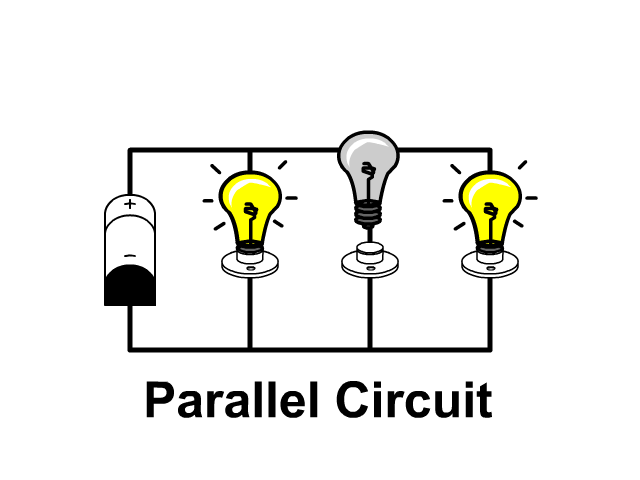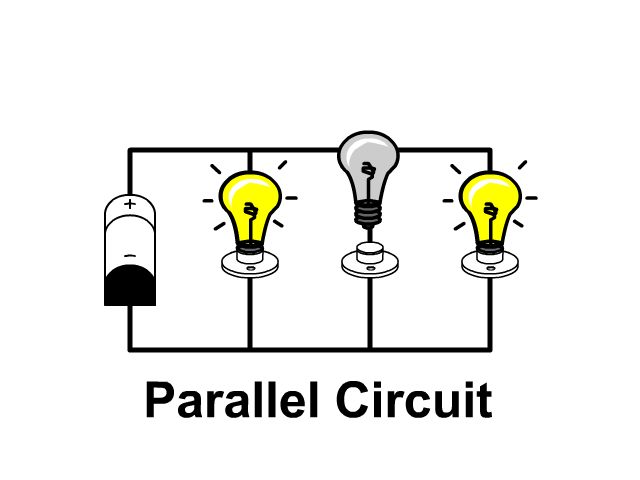
Series Circuits only have one path while parallel circuits we will see in a later unit have branches.  Compare the pictures below each with three resistors.

Series Circuit No Branches

Lights in a Series Circuit Compared to a Parallel Circuit

When lights are connected in a series circuit and one goes out the circuit becomes open and no other light works.  This is because there is no path to the negative terminal of the battery when a circuit is open.

When lights are connected in parallel circuit and one light goes out the remaining ones stay on.  No current will flow down the branch with the disconnected light bulb since that branch is open.  Current will follow the other paths to the negative terminal of the battery leaving the other lights on.

Series Circuit Diagrams

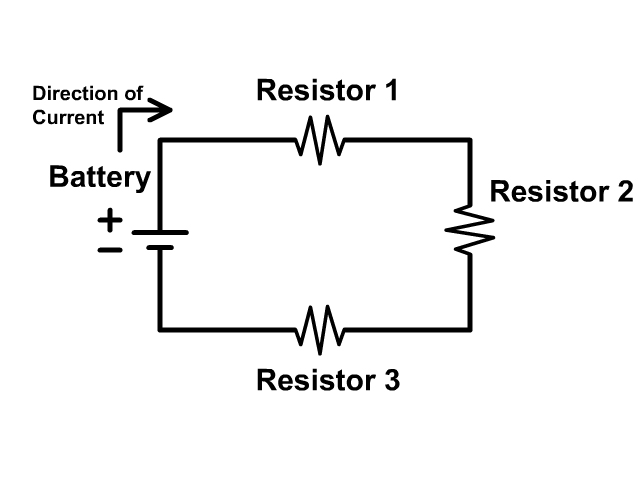
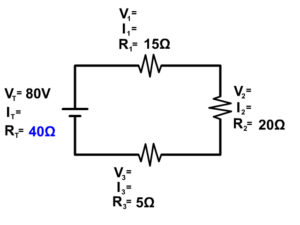
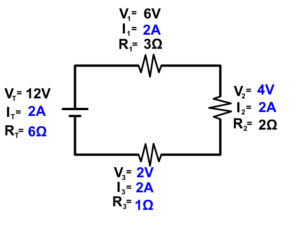
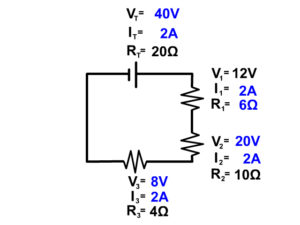
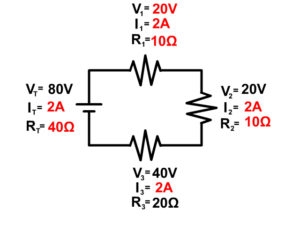
To keep the models simple we will only places a battery and resistors in the circuits of our diagrams on this page.  Remember that the longer line in the battery symbol is the positive terminal and the shorter line is the negative terminal.  The convention is to have current run from the positive terminal to the negative terminal.  Due to this convention the resistors are numbered in order.  Here the resistors get their number resistor 1, resistor 2, and resistor 3 based on the flow of current starting from the positive terminal of the battery.

Series Circuit Rules

Voltage Drop In A Series Circuit

In a series circuit voltage drops across each resistor until the entire amount provided by the battery has dropped.  If you add all the individual voltage drops of a series circuit together you can determine the voltage of the entire circuit (VT) found at the power source.

VT = V1 + V2 + V3 + …

Current in a Series Circuit

There is only one path in a series circuit for current to travel on.  All current must run from the positive terminal to the negative terminal of the power source.  Observe the animation of how the same current has to flow through every component of the circuit in series.

IT = I1 = I2 = I3 = …

Resistance in a Series Circuit

Any resistor or load (device with a resistance) in a series acts like a speed bump in a series slowing current down.  Since there is only one conductive path in series every device adds to total resistance.

RT = R1 + R2 + R3 + …

Note that a wire itself has resistance and the less conductive a wire is the more resistance it would add to a circuit.  We will ignore this in our examples below for simplicity and pretend the wire was 100% conductive.

Circuit Equations

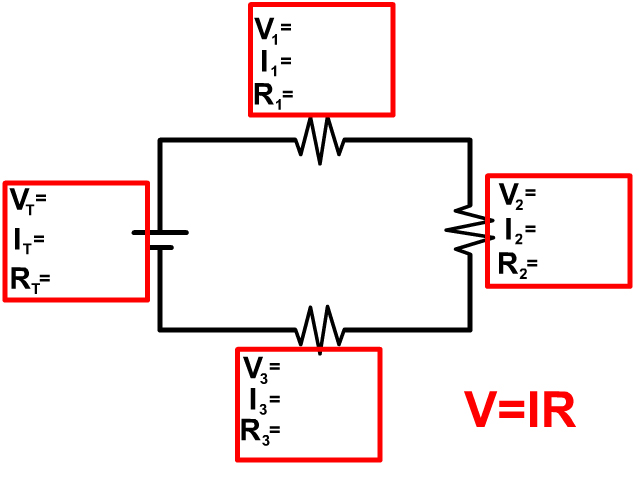
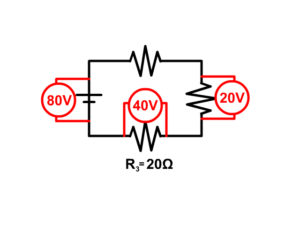
Ohm's Law (V=IR), Voltage equals current times resistance, can be used anywhere in the circuit but only at a single location.

See all the squares in red above, if you are using Ohm's law you can only use information in that location, the V,I, and R within a single square.

The location can be an individual resistor, for example resistor one with the variables Voltage (V1), Current (I1), Resistance (R1).  The location can also be at the battery, which is a measure that represents the overall circuits voltage (VT), current (IT), and Resistance (RT).

At the battery the subscript T (ex. VT) stands for total or of the circuit.  Some equations sheets may use emf (ex. Vemf) or another notation, if there is any subscript other than a number it will likely be of the circuit.

When you are using information between different red blocks you must use the series circuit rules.

VT = V1 + V2 + V3 + …

IT = I1 = I2 = I3 = …

RT = R1 + R2 + R3 + …

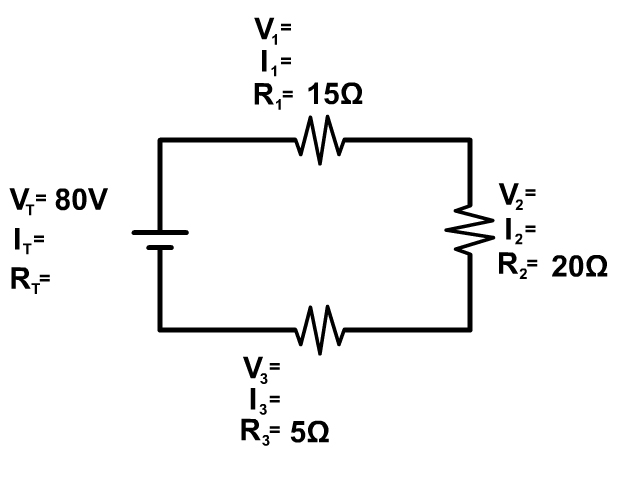
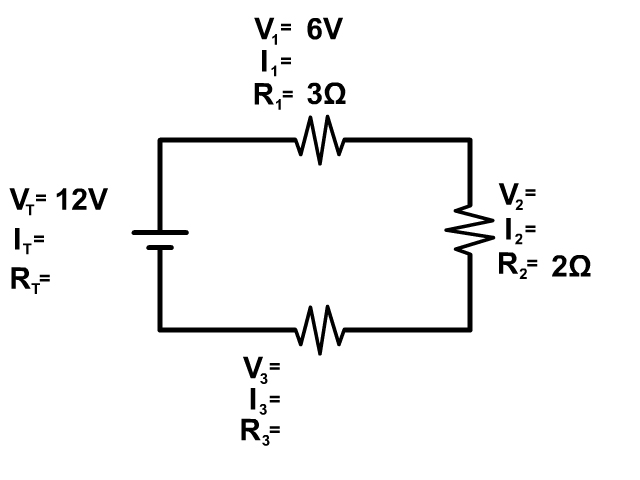
Start any problem by drawing out the circuit and have every resistor labeled as you see in the picture above.  Then write in all your givens.  Next, follow the basic steps to a series circuit problem.

Basic Steps To A Series Circuit Problem

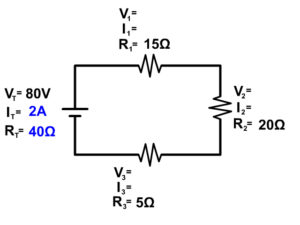
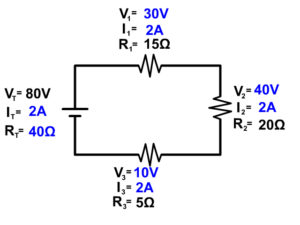
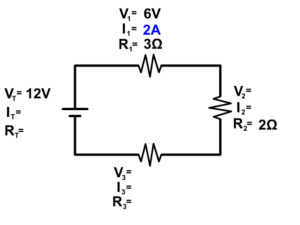
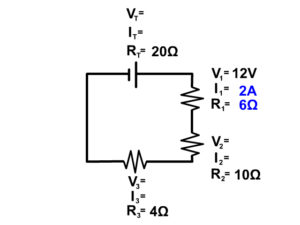
#1 See if you can do Ohm's Law (V=IR) at any location in the circuit.

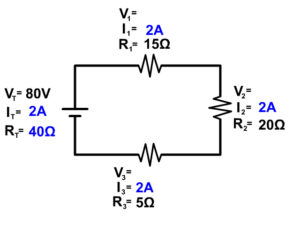
#2 See if you have current anywhere because that current will be the same everywhere following the series circuit rule below.

IT = I1 = I2 = I3 = …

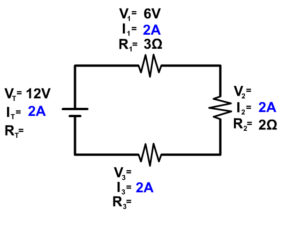
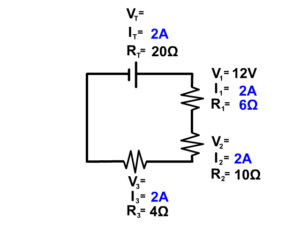
#3 Check if you can do any of the other series circuit rules.

VT = V1 + V2 + V3 + …

RT = R1 + R2 + R3 + …

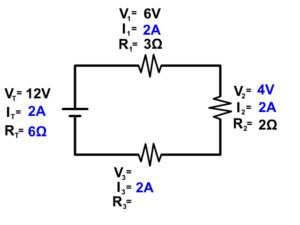
You will continue to follow these steps over and over until everything in the circuit is complete.  Follow our examples below until you feel comfortable to follow the steps solving series circuit problems on your own.

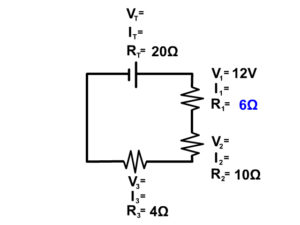
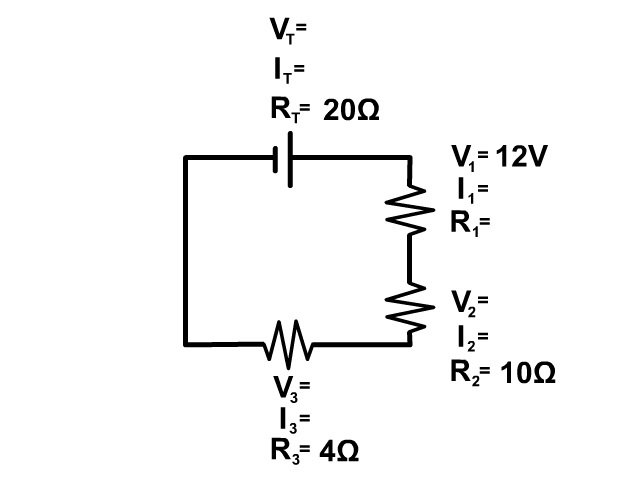
Example Problem 1

Here we don't have enough information to use Ohm's Law (V=IR) at any location so we need to look at the series circuit equations

VT = V1 + V2 + V3 + …

IT = I1 = I2 = I3 = …

RT = R1 + R2 + R3 + …

We can use the last of the equations to solve for the resistance of the circuit (at the battery first).  We only have three resistors so we leave off any other part not in this circuit from the equation

RT = R1 + R2 + R3

RT = 15Ω + 20Ω + 5Ω = 40Ω

step 1

Now we have enough information to use Ohm's law at the battery to determine the current (IT) at the battery

IT=VT/RT

IT=80V/40Ω = 2A

step 2

Now that we know current at any location, in this case the battery, we know it everywhere in a series circuit

IT = I1 = I2 = I3

IT = 2A

I1 = 2A

I2 = 2A

I3 = 2A

step 3

Now we have enough information to solve for voltage everywhere using Ohm's Law (V=IR)

V1 = I1 x R1

V1 = 2A x 15Ω = 30V

 

V2 = I2 x R2

V2 = 2A x 20Ω = 40 V

 

V3 = I3 x R3

V3 = 2A x 5Ω = 10 V

step 4

It is important to make one final check.  Since we finished using Ohm's Law to solve for V3, lets make sure this last step also fits with the series circuit rule.

VT = V1 + V2 + V3

80V = 30V + 40V + 10V

This is also mathematically correct so we know we solved for all the parts of this circuit correctly.  If it did not we would know we had an error and would have to trace back our steps or starting over is sometimes easier.

Example Problem 2

Note:  While our example stick to whole numbers for simplicity, this would be very uncommon and you would normally have decimals.  Do not be shocked if you have decimals, just make sure all the rules are followed and do a final check as presented in the examples below.

You have enough information to start this circuit at the first resistor using Ohm's Law (V=IR)

V1 = I1 x R1 rearranges to I1 = V1/R1 when solving for current.

I1 = 6V/3Ω = 2A

step 1

Now that we know current at the at one location, the first resistor, we know it's the same everywhere following series circuit rules.

IT = I1 = I2 = I3

2A = 2A = 2A = 2A

step 2

Now we have enough information to use Ohm's Law (V=IR) to solve for resistance of the circuit (at the battery) and voltage at resistor 2

VT = IT x RT rearranges to RT = VT/IT

RT = VT/IT

RT = 12V/2A = 6Ω

 

V2 = I2 x R2

V2 = 2A x 2Ω = 4V

Now our circuit looks like this

step 3

From here we can solve for either voltage or resistance of resistor 3 using the overall series circuit rules.

VT = V1 + V2 + V3

12V = 6V + 4V + V3

V3 = 12V - 6V - 4V

V3 = 2V

 

RT = R1 + R2 + R3

6Ω = 3Ω + 2Ω + R3

R3 = 6Ω  - 3Ω - 2Ω

R3 = 1Ω

step 4

Since we solved for R3 last using series circuit rules do the final check at resistor three making sure it follows Ohm's Law at this location as well.

V3 = I3 x R3

2V = 2A x 1Ω

It makes the final check so we know we solved for the parts of this circuit correctly.

Example Problem 3

Series Circuit Example Problem 3

In this circuit we don't have enough information to start with Ohm's Law since we don't have two out of three parts of Ohm's Law at any one location.

We do have enough information to start with the series circuit resistor rule.  RT = R1 + R2 + R3

RT = R1 + R2 + R3

20Ω = R1 + 10Ω + 4Ω

R1 = 20Ω - 10Ω - 4Ω = 6Ω

Our circuit now looks like this

step 1

Now we can solve for current at resistor 1 using Ohm's Law

V1 = I1 x R1

I1 = V1/R1

I1 = 12V/6Ω = 2A

step2

Now that we know current in one location we know the current everywhere in the circuit following the series circuit rules.

IT = I1 = I2 = I3

2A = 2A = 2A = 2A

Our circuit now looks like this

step 3

Now use Ohm's Law (V=IR) to solve for all the remaining components since we have enough information to do so.

VT = IT x RT

VT = 2A x 20Ω = 40V

 

V2 = I2 x R2

V2 = 2A x 10Ω = 20V

 

V3 = I3 x R3

V3 = 2A x 4Ω = 8V

Our circuit now looks like this

step 4

Since we ended by solving for V3 using Ohm's Law, our final check is to make sure voltage also follow the series circuit rules for voltage.

VT = V1 + V2 + V3

40V = 12V + 20V + 8V

This is a correct mathematical statement so we know we solved our series circuit correctly.

Notice the following about some series circuit problems

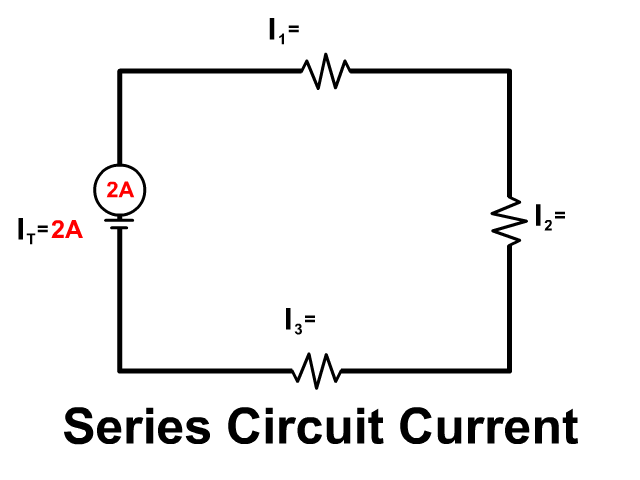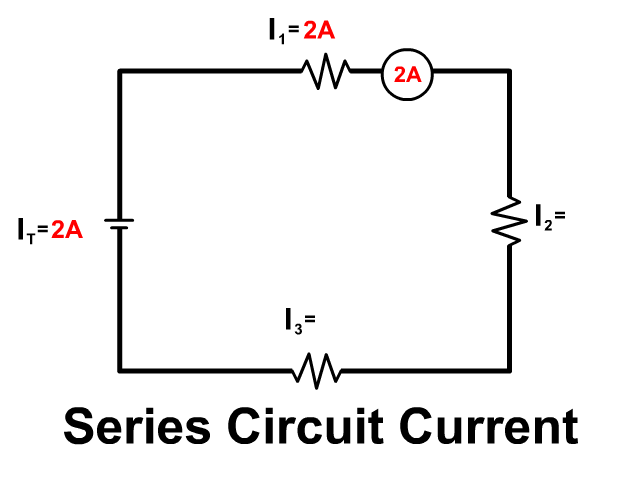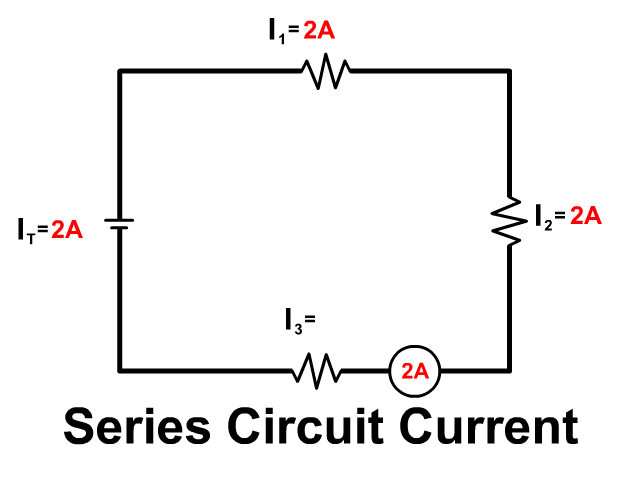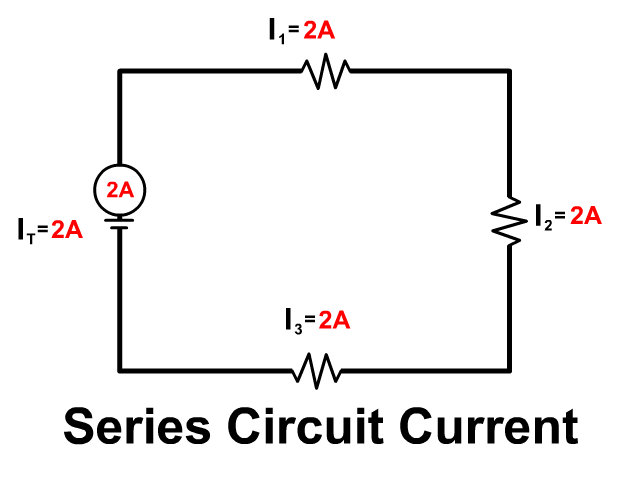
Some problems as the one seen below are drawn showing multimeters taking the reading of the current as seen below.  This is not part of the circuit and is just taking a reading.

Series Circuit Exmple 4 Drawn With Multimeters

You would rewrite the problem above taking out the multimeters and placing the readings into the problem and start the problem as seen in example 4 below.

Example Problem 4

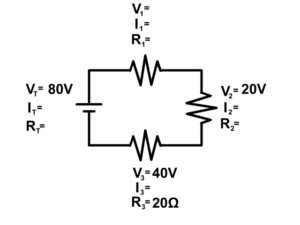
Series Circuit Example 4

Try example 4 on your own and click "See Solution" to check your answers.

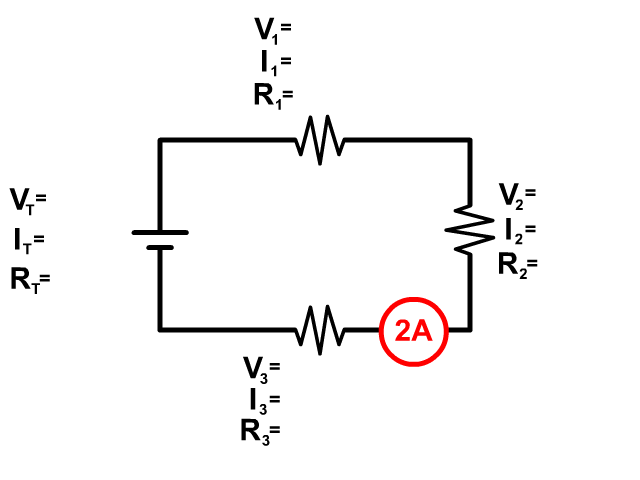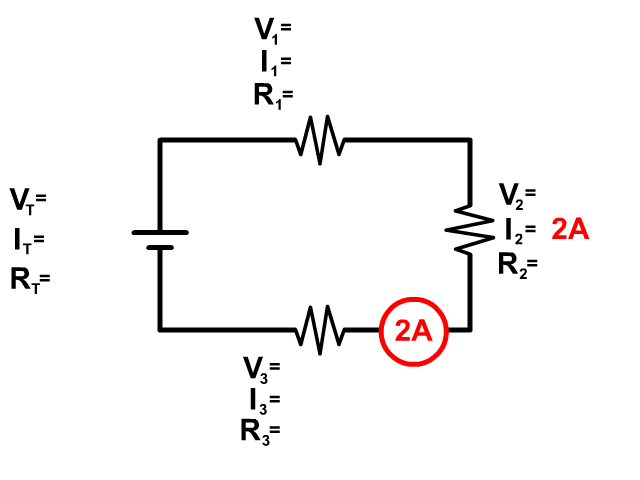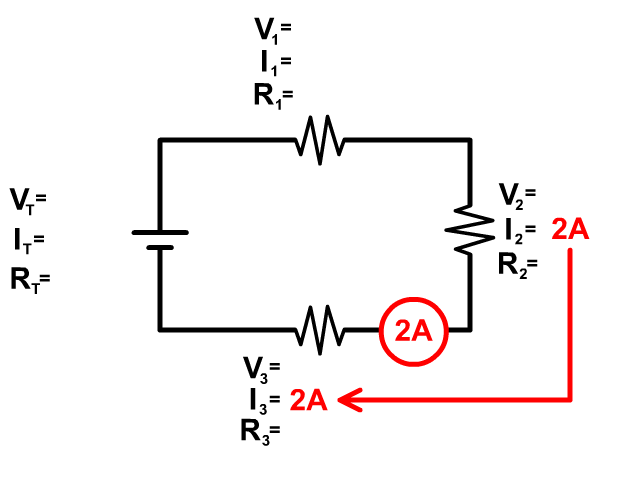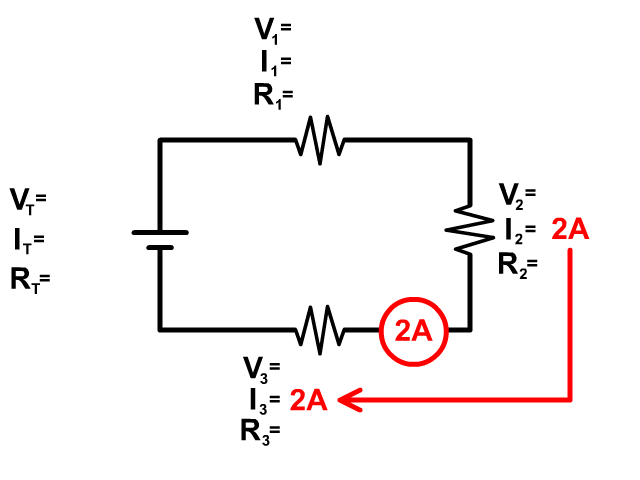
Another Way Current Can Be Given In A Series Circuit Problem

Be aware that current can also be drawn into a problem in the wire and not at a single resistor.  This is not an additional resistor but seeing the current drawn as a circle over the wire shows you the current in that wire.  Since there is only one wire going from the previous resistor to the new resistor, you know in series both of those must have that current as well.  See the picture to see a visual of this.

Circuit Construction Kit

The following PhET circuit construction kit can help you understand the workings of circuits more.

CLICK HERE FOR THE SERIES CIRCUIT LAB SHEET

Go to the following website is the embedded version is not working

https://phet.colorado.edu/sims/html/circuit-construction-kit-dc/latest/circuit-construction-kit-dc_en.html

Links

Terms and Conditions - Privacy Policy